Chess tournament with 1.5 Points Winners

Consider the participants as the nodes of a graph. Join two nodes with a blue edge if the game between the two players ended in draw; join two nodes with a red edge if on of the players won the game.

As the simplest example of Ramsey's theory, with the number of participants $n\ge 6,$ there is always a monochromatic triangle. In such a triangle, either all three games ended with a draw, or all three ended with a win for one of the players. In either case, there's no participant who got $1.5$ points against two other players.

For five participants it is possible to satisfy the conditions of the problem:

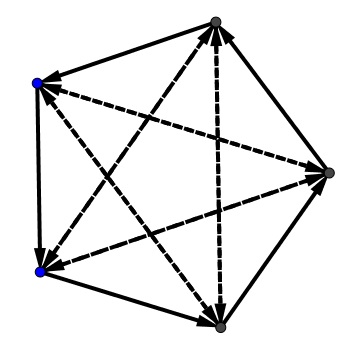
In the diagram, all outer edges are similarly oriented and the direction of the vectors is, say, from the winner to the loser. All dashed, internal edges designate the games that ended in a draw.

This is problem CC124, the Contest Corner, from the Crux Mathematicorum. The commentary at VOLUME 41, NO. 5 May 2015 reports that "Originally that was question 3 on the 1999 entrance exam to the mathematical-mechanical department of the Belorussian State University. We received no solutions to this problem."