Ramsey's Number R(5, 3)

Ramsey's Number R(5, 3) is the least integer N that solves the following problem

In any group of N people either there are 5 that know each other or there are 3 that do not know each other.

There is a symmetry in the definition: the properties of knowing and not-knowing each other can be swapped:

In any group of N people either there are 3 that know each other or there are 5 that do not know each other.

Proposition

R(5, 3) = 14.

Proof

First, we show that R(5, 3) ≤ 14. This follows from the general inequality

R(m, n) ≤ R(m-1, n) + R(m, n-1),

which gives R(5, 3) ≤ R(5, 2) + R(4, 3) = 5 + 9 = 14.

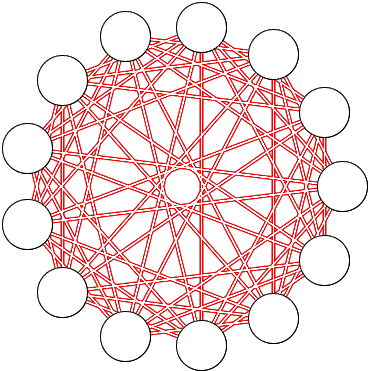
Second, we exhibit a group of 13 which does not posses the required property. To this end, we shall use a bichromatic graph interpretation for the group of people where to nodes are joined by an edge iff the two persons they represent are acquainted.

In the graph below contains all the chords of lengths other than 1 and 5. There are no five nodes that form a K₅, a 5-node complete graph.

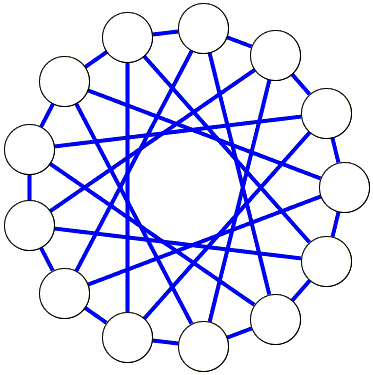
The complementary graph contains no triangles:

Note: I am grateful to Stephanie Lewis for pointing out an error in an earlier version of the page and for providing the reference to J. G. Kalbfleisch' paper.

References

1. V. K. Balakrishnan, Theory and Problems of Combinatorics, Schaum's Outline Series, McGraw-Hill, 1995, pp. 22-25
2. J. G. Kalbfleisch, Construction of Special Edge-Chromatic Graphs, Canadian Math. Bull. vol. 8, no. 5, October 1965, 575-584

1. Ramsey's Theorem
2. Party Acquaintances
3. Ramsey Number R(3, 3, 3)
4. Ramsey Number R(4, 3)
5. Ramsey Number R(5, 3)
6. Ramsey Number R(4, 4)
7. Geometric Application of Ramsey's Theory
8. Coloring Points in the Plane and Elsewhere
9. Two Colors - Two Points
10. Three Colors - Two Points
11. Two Colors - All Distances
12. Two Colors on a Straight Line
13. Two Colors - Three Points
14. Three Colors - Bichromatic Lines
15. Chromatic Number of the Plane
16. Monochromatic Rectangle in a 2-coloring of the Plane
17. Two Colors - Three Points on Circle
18. Coloring a Graph
19. No Equilateral Triangles, Please

|Contact| |Front page| |Contents| |Algebra| |Store|

Copyright © 1996-2012 Alexander Bogomolny