Party Acquaintances

An interesting problem has entered mathematical folklore in the 1950s. It was included in the Putnam Competition in 1953 and posted in the problem section of the American Mathematical Monthly in 1958 (Problem E 1321). Martin Gardner wrote about it on three different occasions. While proving an extension of the problem, Paul Erdös came up with his probabilistic method.

Prove that at a party of six people either there are three mutual acquaintances or there are three mutual strangers.

(This is sometimes known as the Friendship Theorem, a Theorem on Friends and Strangers, or Ramsey's Theorem in honor of the Cambridge University mathematician Frank Plumton Ramsey who died in 1930 when only 26.)

The problem is naturally modelled on a 2-color graph. To remind, K_n is the standard notation for a complete graph with n vertices. Assume the edges of K₆ are all colored into two colors: red or blue. The problem is equivalent to the statement that for any such coloring there is always a monochromatic triangle (a K₃). In fact, it has been shown by A. W. Goodman (1959) that the number of monochromatic triangles is at least 2!

The applet allows to experiment with the problem and its generalizations. To draw an edge, click on one of the nodes, move the cursor to another node, and click there too. If the AutoColor box is checked, the edges are drawn with alternating colors. Otherwise, you can choose color to draw an edge with by checking either Red or Blue box.

On K₅ there exist bichromatic colorings without monochromatic K₃ subgraphs. (Think of five people sitting by a round table such that each of them is friends only with his immediate neighbors.) Therefore, 6 is the smallest number k with the property that, for any bichromatic coloring, K_k contains either red K₃ or blue K₃. This is written as

(*)

R(3, 3) = 6,

(Note that the Friendship Theorem states that R(3, 3) ≤ 6.) In general, the Ramsey number R(n, m) is the smallest number N such that, for any bichromatic coloring of K_N, there is either red K_n or blue K_m. As an example, it is obvious that, for any m > 1, R(2, m) = m. Also, R(m, n) = R(n, m).

It is also known that

(**)	R(4, 3) = 9, R(5, 3) = 14, R(4, 4) = 18, R(6, 3) = 18, R(7, 3) = 23 R(5, 4) = 25.

The latter result has been established in 1993 and published in 1995. The initial announcement of the result was made, of all places, on the pages of Rochester Democrat and Chronicle. Somebody sent a letter to Ann Landers who published it in her syndicated advisory column. She ended her reply with 'I am "Baffled in Chicago"' [Gardner, pp. 452-453].

The exact value of R(5, 5) is still unknown, except for the bounds

42 < R(5, 5) < 50.

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

Party Acquaintances

What if applet does not run?

In the 1960s, Gustavus J. Simmons redressed (*) as a game, that became known as the Game of Sim [Gardner, p. 111]. In the game, two players alternate drawing edges of two colors. The loser is the player who first creates a triangle of his or her color. Since (*) has been shown to be correct, Sim can't end in a draw. Since K₆ has 15 edges and 15 is an odd number, the second player has an obvious advantage. However, the game is not quite trivial and several strategies have been published in the 1970s in the Journal of Recreational Mathematics and Mathematics Magazine.

Martin Gardner mentions an observation by F. Harary that (*) affords at least three other types of games. He classified the SIM as the game of avoidance. In the game of achievement the player to complete a monochromatic triangle first wins. This game is trivial. But the other two are not. In the latter games the play continues until all the edges are drawn, after which the players count the number of triangles of their color. The winner may be the player with the most or fewest number of triangles. These last two games are the hardest to analyze.

Helpful in proving (**) is a recursive inequality:

(1)

R(m, n) ≤ R(m-1, n) + R(m, n-1).

For the proof [Balakrishnan, 1.98], introduce r = R(m-1, n) + R(m, n-1) and consider a company {1, 2, ..., r} of r people. Let M be the set of people known to person 1 and N be set of people not known to person 1. Between them, M and N have r-1 persons. Therefore, either M has at least R(m-1, n) people or N has at least R(m, n-1) people. Assuming the former, M then has at least m-1 people who know each other or n people who do not know each other. Thus we either have n people who do not know each other or (adding person 1 to M) m people who know each other. Assuming that N has at least R(m, n-1) people we, by symmetry, are led to the same conclusion.

In case R(m-1, n) and R(m, n-1) are both even (1) can be strengthened [Balakrishnan, 1.100]:

(2)

R(m, n) ≤ R(m-1, n) + R(m, n-1) - 1.

To see this, set p = R(m-1, n), q = R(m, n-1) and r = p + q. Consider a group X = {1, ..., r-1} of r-1 people. We wish to show that either X contains m mutual acquaintances or it contains n mutual strangers. Let d_i be the number of people known to person I. Since being an acquaintance is a mutual relationship, the sum Sd_i of all d_i's is even. However, by our assumption, r is even, so that r-1 is odd. It follows that d_i ought to be even for at least one person. For the definiteness sake, suppose d₁ is even and let M and N be the sets of all people known and, respectively, not known to person 1. Denoting the number of elements in a set X as |X|, |M| = d₁, an even number. Since |M| + |N| = r-2, |N| is also even. Further, either M has at least p-1 people or N has at least q people. But p-1 is odd, while |M| is even; thus we can strengthen the above sentence: either M has at least p people or N has at least q people. But if |M| ≤ p (= R(m-1, n)), M then contains either m-1 acquaintances or n strangers. Together with person 1, X has either m acquaintances or n strangers. And we are done in this case. The other is treated similarly.

Thus, for example, the second inequality is used to show that R(4, 3) ≤ R(3, 3) + R(4, 2) - 1 = 9. In fact, Ramsey Number R(4, 3)R(4, 3) = 9.

As another example, by (1),

R(5, 3) ≤ R(4, 3) + R(5, 2) = 9 + 5.

To see that R(5, 3) > 13, imagine 13 people sitting at a round table such that each person is acquainted only with the fifth person on his left and the fifth person on his right. Under this assumption, there is no 3 mutual acquaintances and no 5 mutual strangers.

R(m, n) with m, n > 2 are known as nontrivial Ramsey numbers.

Ramsey numbers R(m, n) exist for all positive integers m and n; moreover,

R(m, n) ≤ C(m + n - 2, m - 1),

where C(x, y) is a binomial coefficient. One proof follows by a straightforward induction from (1).

There are also generalizations. Let k_i, i = 1, 2, ..., t, and m be positive integers satisfying k_i ≤ m and t ≥ 2. Let C be the collection of all m-element subsets of an n-element set X. |C| = C(n, m). Let C₁, ..., C_t be an ordered partition of C. Then n is said to possess the generalized (k₁, k₂, ..., k_t; m)-Ramsey property if, for some I, X has a k_i-element subset B such that all m-element subsets of B belong to C_i. The smallest such n is called the generalized Ramsey number, R(k₁, k₂, ..., k_t; m).

R(u, v) = R(u, v; 2). To see that, consider X = {1, 2, ..., n} and the collection C of its 2-element subsets. For a partition C = C₁ ∪ C₂, think of C₁ and C₂ as containing pairs of mutual acquaintances and mutual strangers. If n = R(u, v), then either X has a group of u acquaintances or a group of v strangers. In the former case, we get a subset B of X, |B| at least u, such that all 2-element subsets of B belong to C₁. In the latter case, a subset B exists with at least v elements, such that all its 2-element subsets belong to C₂. This implies that n = R(u, v) has the generalized R(u, v; 2)-Ramsey property. From the definition it also follows that n is the least such number.

The existence of R(k₁, k₂, ..., k_t; m) is claimed by Ramsey's theorem which is a fundamental part of an extensive Ramsey theory. The theory is concerned with the emergence of certain properties in objects as their scale becomes large. As a rather simple example, the pigeonhole principle is equivalent to the statement:

R(k₁, k₂, ..., k_t; 1) = k₁ + k₂ + ... + k_t - t + 1.

The Friendship theorem itself has a curious application [Savchev, pp. 146-147, Honsberger, p. 3]. Six random points in space are joined pairwise by 15 line segments. Assume all the segments are of different length. Some segments form triangles. Prove that at least one of the 15 segments serves as the shortest side in one of the triangles it is in, and as the longest side in another. Six points taken by three form 20 triangles. In each, let's color the shortest side in red. It may happen that some of the sides will be painted more than once. Let's color the remaining segments blue. By the Friendship theorem, there is a monochromatic triangle. Since the triangle has a shortest side that had to be colored red, the whole triangle is red. In particular, its longest side is red as well. The fact that it is red means it's the shortest side in some other triangle.

The numbers R(3, 3, ..., 3; m) with m 3s are often denoted R_m. (And sometimes it is m that gets omitted: R(3, 3, ..., 3).) R_m is the minimum number of dots in a complete graph such that if the graph's edges are colored with m colors, there is bound to be at least one monochromatic triangle. R(3, 1) = 3. R(3, 3; 2) = R(3, 3) = 6. R(3, 3, 3; 3) = 17. Although the exact values of R_m are mostly unknown, it can be shown that their values are sharp!

Note

Here's an example of a graph with 6 nodes and 14 edges (a complete graph minus one edge) that could be colored with two colors without forming monochromatic triangle:

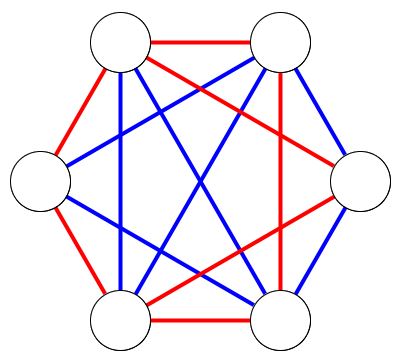
Golomb's example of a 6-node graph with 14 edges

Reference

M. Aigner, G. Ziegler, Proofs From The BOOK, Springer, 2000
R. B. J. T. Allenby, A. Slomson, How to Count: An Introduction to Combinatorics, CRC Press, 2011 (2nd edition)
V. K. Balakrishnan, Theory and Problems of Combinatorics, Schaum's Outline Series, McGraw-Hill, 1995
M. Gardner, The Colossal Book of Mathematics, W. W. Norton & Co, 2001
M. Gardner, Knotted Doughnuts and Other Mathematical Entertainments, W.H.Freeman & Co., 1986.
M. Gardner, The Unexpected Hanging and Other Mathematical Diversions, The University of Chicago Press, 1991
M. Gardner, The Colossal Book of Short Puzzles and Problems, W. W. Norton & Company, 2006, p. 10
A. W. Goodman, On Sets of Acquaintances and Strangers at Any Party, Am Math Monthly, v. 66, no. 9 (Nov., 1959), 778-783.
P. Hilton, D. Holton, J. Pederson, Mathematical Vistas, Springer, 2002
R. Honsberger, Mathematical Delights, MAA, 2004
L. E. Shader, Another Strategy for SIM, Math Magazine, v. 51, No. 1 (Jan., 1978), pp. 60-64
S. Savchev, T. Andreescu, Mathematical Miniatures, MAA, 2003
A. Soifer, Geometric Etudes in Combinatorial Mathematics, Springer, 2010 (2nd, expanded edition)

71878576