Chromatic Number of the Plane

If a plane is colored in two colors then, for any unit of length, there is a monochromatic pair of points, i.e. a pair of points of the same color, at exactly the unit distance from each other. This is actually true even if the plane is colored with 3 colors.

Definition

The smallest number of colors needed in a coloring of the plane to ensure that no monochromatic pair is at the unit distance apart is called the chromatic number χ of the plane.

From the results just mentioned, χ ≥ 4. This is quite easy to show that χ ≤ 7. Indeed, pick up a parahexagon. Parahexagons are known to tile the plane. For a start, surround one of them with six others and assign each a different color, as shown below:

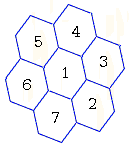
7 hexagons with 7 colors

The resulting 18-gon also tiles the plane and leads to the coloring of the plane with 7 colors.

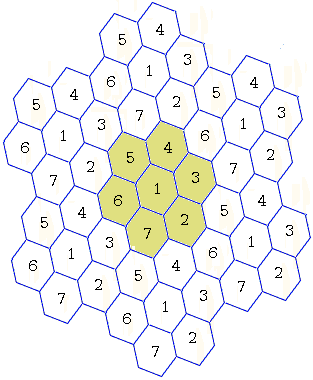
tiling the plane with hexagons

Now it is clear that the tiling can be rescaled to avoid a monochromatic pair for any given unit of length.

Theorem

4 ≤ χ ≤ 7.

Interestingly, no progress was made on the low estimate until 2018, when the de Grey Graph raised the lower bound to 5. The Parts Graph of 509 vertices is the smallest known 5-chromatic graph.

Remark

A chromatic number could be (and is) associate with sets of points other than the plane. For example, a chromatic number of a graph is the minimum number of colors which are assigned to its vertices so as to avoid monochromatic edges, i.e., the edges joining vertices of the same color. It is known that, for a planar graph, the chromatic number is at most 4.

References

  1. V. Klee, S. Wagon, Old And New Unsolved Problems, MAA, 1991
  2. A. Soifer, Geometric Etudes in Combinatorial Mathematics, Springer, 2010 (2nd, expanded edition)
  1. Ramsey's Theorem
  2. Party Acquaintances
  3. Ramsey Number R(3, 3, 3)
  4. Ramsey Number R(4, 3)
  5. Ramsey Number R(5, 3)
  6. Ramsey Number R(4, 4)
  7. Geometric Application of Ramsey's Theory
  8. Coloring Points in the Plane and Elsewhere
  9. Two Colors - Two Points
  10. Three Colors - Two Points
  11. Two Colors - All Distances
  12. Two Colors on a Straight Line
  13. Two Colors - Three Points
  14. Three Colors - Bichromatic Lines
  15. Chromatic Number of the Plane
  16. Monochromatic Rectangle in a 2-coloring of the Plane
  17. Two Colors - Three Points on Circle
  18. Coloring a Graph
  19. No Equilateral Triangles, Please

|Contact| |Front page| |Contents| |Coloring Plane|

Copyright © 1996-2018 Alexander Bogomolny

71878447