Ramsey's Number R(3, 3, 3)

In general, the Ramsey number R(p₁, p₂, ..., p_n; k), where k and p₁, p₂, ..., p_n are positive integers, is the least such N that a complete graph K_N colored into k colors, has a monochromatic subgraph K_{p_s} for at least on 1 ≤ s ≤ k. Where n = k, k is usually omitted: R(p₁, p₂, ..., p_n); and when all p's are equal, the notation is further shortened to R(p), or R_p. Thus, say, R(3) stands for R(3, 3, 3) which in turn is the same as R(3, 3, 3; 3).

According to [Gardner, p. 443] it was first proved in 1955 that R(3) = 17; but already in 1964 the problem has been offered at the International Mathematical Olympiad.

Below, we shall first prove that R(p₁, p₂, ..., p_n) exists and then proceed to establish the value for R(3).

Ramsey's Theorem

Suppose p₁, p₂, ..., p_n are positive integers. Then there exists an integer R(p₁, p₂, ..., p_n) such that if v ≥ R(p₁, p₂, ..., p_n), then any coloring of the edges of K_v with n colors will contain a subgraph K_{p_s} with all edges of color s, for at least on s.

Proof

See [Allenby & Slomson, Theorem 16.10; Wallis & George, 3.3].

From R(m, n) ≤ R(m-1, n) + R(m, n-1) it follows that the theorem holds for n = 2. To apply mathematical induction, assume that it holds for n = t-1. Then p₀ = R(p₂, ..., p_n) exists. Select v ≥ R(p₀, p₁) and color K_v in colors 1, 2, ..., t. Then replace colors 2, 3, ..., t with a new color 0. Either there is K_p₀ in color 0 or K_p₁ in color 1. In the latter case we are done. In the former, return the just found K_p₀ to the original colors. By the inductive hypothesis K_p₀ contains a monochromatic graph K_{p_s} for some s from 2 ≤ s ≤ t.

What we actually proved could be expressed as

R(p₁, p₂, ..., p_n) ≤ R(p₁, R(p₂, ..., p_n)).

So, in particular, R(3) = R(3, 3, 3) ≤ R(3, R(3, 3)) = R(3, 6) = 18. A problem offered at the 1964 International Mathematical Olympiad claims that R(3) ≤ 17:

Theorem

Each of 17 students talked with every other student. They all talked about three different topics. Each pair of students talked about one topic. Prove that there are three students that talked about the same topic among themselves.

Proof

Denote the topics discussed by the students T₁, T₂, T₃. Consider one of the students, say A. Since A talked about three topics to 16 other students, by the Pigeonhole Principle, there are at least 6 students with whom A talked of a single topic, say, T₁. Then there are just to possibilities. If any pair from the 6 students discussed topic T₁ we are done. Otherwise, there are 6 students that discussed between themselves only 2 topics - T₂ or T₃. So we are looking at the number R(3, 3) which is 6; and we are done in this case also.

To prove that indeed R(3) = 17 requires to exhibit a coloring of K₁₆ in three colors with no monochromatic triangle. Such a graph exists and is formed by three overlapping copies of the Clebsch graph, each of which is colored in one of the three given colors.

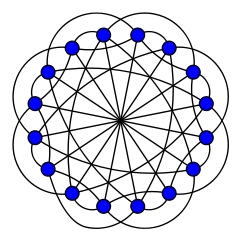
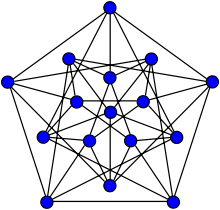
Reference

R. B. J. T. Allenby, A. Slomson, How to Count: An Introduction to Combinatorics, CRC Press, 2011 (2nd edition)
D. Djukić et al, The IMO Compendium, Springer, 2011 (Second edition)
M. Gardner, The Colossal Book of Mathematics, W. W. Norton & Co, 2001
W. D. Wallis, J. C. George, Introduction to Combinatorics, Chapman and Hall/CRC, 2010, p. 52

41162543