Ramsey's Number R(4, 4)

Noga Alon and Michael Krivelevich [The Princeton Companion to Mathematics, p. 562] present a story of the Ramsey number R(4, 4),

In the course of an examination of friendship between children some fifty years ago, the Hungarian sociologist Sandor Szalai observed that among any group of about twenty children he checked he could always find four children any two of whom were friends, or else four children no two of whom were friends. Despite the temptation to try to draw sociological conclusions, Szalai realized that this might well be a mathematical phenomenon rather than sociological one. Indeed, a brief discussion with the mathematicians Erdös, Turán, and Sós convinced him this was the case.

The phenomenon Szalai has observed falls into the purview of Ramsey's theory, while 20 is a rough estimate to the Ramsey number R(4, 4).

Proposition

For any graph G with at least 18 nodes, either G or its complement Gc, contain complete subgraph K4 of four nodes.

Proof

Pick a node, say, A. The nodes of G are split into two groups: those that are joined to A (group S) and those that are not (group T). Either |S| ≥ 9 or |T| ≥ 9.

If |T| ≥ 9, then either there is in T K4 or three mutually disjoint nodes. In the former case, we immediately have a K4. In the latter case, adjoining A to the three disjoint nodes, shows the existence of K4 in Gc.

If |S| ≥ 9, we use the fact that R(4, 3) = R(3, 4) to claim that either there is in S K3 or four mutually disjoint nodes. In the latter case, we immediately have a K4 in Gc. In the former case, adjoining A to K3 in S shows the existence of K4 in G.

Theorem

R(4, 4) = 18.

Proof

For a proof we only need to exhibit a 17-node graph G such that neither G nor Gc contain K4.

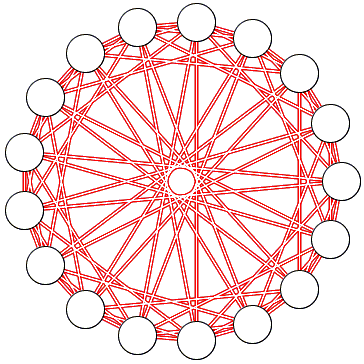
Ramsey number R(4, 4) - counter example on 17 nodes

Place 17 nodes on a circle and join all the chords of lengths 1, 2, 4, and 8.

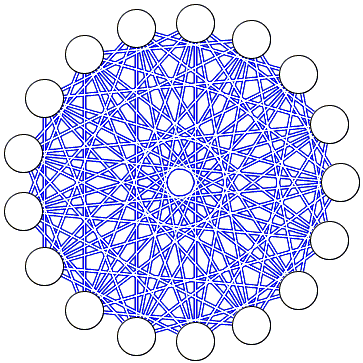
Ramsey number R(4, 4) - complementary graph

The complementary graph consists of chords of lengths 3, 5, 7, and 11.

Note: I am grateful to Stephanie Lewis for pointing out an error in an earlier version of the page and for providing the reference to J. G. Kalbfleisch' paper.

References

  1. V. K. Balakrishnan, Theory and Problems of Combinatorics, Schaum's Outline Series, McGraw-Hill, 1995, pp. 22-25
  2. T. Gowers (ed.), The Princeton Companion to Mathematics, Princeton University Press, 2008, p. 562
  3. J. G. Kalbfleisch, Construction of Special Edge-Chromatic Graphs, Canadian Math. Bull. vol. 8, no. 5, October 1965, 575-584

  1. Ramsey's Theorem
  2. Party Acquaintances
  3. Ramsey Number R(3, 3, 3)
  4. Ramsey Number R(4, 3)
  5. Ramsey Number R(5, 3)
  6. Ramsey Number R(4, 4)
  7. Geometric Application of Ramsey's Theory
  8. Coloring Points in the Plane and Elsewhere
  9. Two Colors - Two Points
  10. Three Colors - Two Points
  11. Two Colors - All Distances
  12. Two Colors on a Straight Line
  13. Two Colors - Three Points
  14. Three Colors - Bichromatic Lines
  15. Chromatic Number of the Plane
  16. Monochromatic Rectangle in a 2-coloring of the Plane
  17. Two Colors - Three Points on Circle
  18. Coloring a Graph
  19. No Equilateral Triangles, Please

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny

71878445