Two Colors - Three Points on Circle

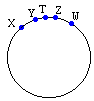
Of any three points two must be of the same color. Therefore, we can definitely find points of the same color as close together as we please. Accordingly, let Y and Z be of the same color and so close that there is room to extend the pair into the ordered quadruple (X, Y, Z, W) of equally spaced points. Let T be the common midpoint of arcs YZ and XW.

For definiteness, assume Y and Z are red. Then, if any X, W, T is also red, a trio of equally spaced red points is determined. Otherwise, (X, T, W) itself is a trio of equally spaced blue points.

Here's a solution by V. Paul Smith, Jr. Consider the vertices of a regular pentagon inscribed in the circle. 3 of the points (at the vertices) have to be the same color. Those 3 points form the vertices of an isosceles triangle, which by definition has two congruent sides. The point common to both matching sides is the midpoint of the sought after trio.