How to Construct Orthogonal Circle

Solution

Below is an applet that is supposed to be suggestive of the construction:

In the applet, you can right-click on the constructed circle and then select trace on. If you do, drag point \(T\) afterwards, you'll see that all the resulting circles orthogonal to \(A(B)\) that pass through \(C\), also pass through another fixed point and have collinear centers on the perpendicular bisector of the segment joining the two points. The second point is the inversion of \(C\) in circle \(A(B).\) To remove the trace, press the Reset button above.

|Contact| |Front page| |Content| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

For points outside the circle, an orthogonal circle emerges from the construction of the tangents from the point to the circle. This construction does not work for points inside the circle. However, from the theory of conjugate pencils of circles, it is rather clear that for any point and any circle there is a multitude of circles through the former, orthogonal to the latter.

If the two circles are orthogonal, the tangents at their common point pass through each other's center.

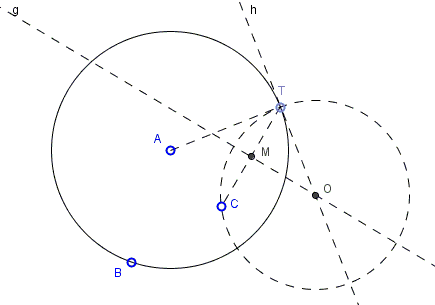
Thus choose any point \(T\) on \(A(B)\) and draw tangent \(h\) to \(A(B)\) at \(T.\) (This is the line orthogonal to the radius \(AT.)\) The center of the sought circle lies on \(h\). In order for a circle to pass through both \(C\) and \(T\) its center must lie on the perpendicular bisector of \(CT\). The intersection \(O\) of the two lines serves as the center of the sought circle, circle \(O(C)\) orthgonal to circle \(A(B).\) (Oviously, this construction works regardless whether the given point is inside or outside the circle.)

For two circles, the center of the circle orthogonal to both needs to lie on the radical axis of the two. The question is to find those that pass through a given point. In general, there is just one. For three circles, there is no choice: the only circle orthogonal to the three given circles is centered at their radical center and has the radius equal to the length of the tangents from the center to the circles. It may or may not pass through a given point.

Related material Read more...
	Various Geometric Constructions
	How to Construct a Radical Axis
	Constructions Related To An Inaccessible Point
	Inscribing a regular pentagon in a circle - and proving it
	The Many Ways to Construct a Triangle and additional triangle facts
	Easy Construction of Bicentric Quadrilateral
	Easy Construction of Bicentric Quadrilateral II
	Star Construction of Shapes of Constant Width
	Four Construction Problems
	Geometric Construction with the Compass Alone
	Construction of n-gon from the midpoints of its sides
	Short Construction of the Geometric Mean
	Construction of a Polygon from Rotations and their Centers
	Squares Inscribed In a Triangle I
	Construction of a Cyclic Quadrilateral
	Circle of Apollonius
	Six Circles with Concurrent Pairwise Radical Axes
	Trisect Segment: 2 Circles, 4 Lines
	Tangent to Circle in Three Steps
	Regular Pentagon Construction by K. Knop

|Contact| |Front page| |Content| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny