Carpets in a Quadrilateral

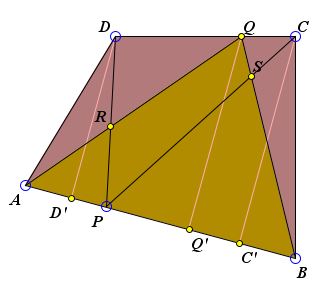
Points P and Q are located on the sides AB and CD of a convex quadrilateral ABCD so that AP/AB = CQ/CD. Let S be the intersection of BQ and CP, R the intersection of AQ and DP. Prove that the blue area (quadrilateral PSQR) equals the sum of the red areas (triangles ARD and BSC.)

Explanation

This is problem #136 from a problem collection by Barbeau, M. S. Klamkin, W. O. J. Moser. The Carpets Theorem is not mentioned in the book and in fact is not needed in the proof. If anything, the proof supplies an additional demonstration for the most general form of the Carpets Theorem.

Denote the common ratio AP/AB = CQ/CD = r. Then

Drop perpendiculars CC', QQ' and DD' from C, Q and D to AB and denote their lengths c, q, and d, respectively. Then

Now,

so that obviously

If we denote AQB as S₁ and CPD as T₁, we'll find that the most general form of the carpets is directly applicable in our case because of (2) which simply states that

The required conclusion follows immediately. However, note that the same result is obtained by subtracting from both sides of (2) the areas of triangles APR and BPS.

References

1. E. J. Barbeau, M. S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges, MAA, 1995, #136

• The Carpets Theorem
• Carpets in a Parallelogram
• Carpets in a Quadrilateral
• Carpets in a Quadrilateral II
• Square Root of 2 is Irrational
• Carpets Theorem With Parallelograms
• Two Rectangles in a Rectangle
• Bisection of Yin and Yang