Carpets in Triangle, II

Problem

Let $D$ be a point on side $BC$ of $\Delta ABC.$ Two lines are drawn through $D$ parallel to the sides of the triangle: $DE\parallel AB,$ $DF\parallel AC,$ $E\in AC,$ $F\in AB.$ The two intersect at point $P.$

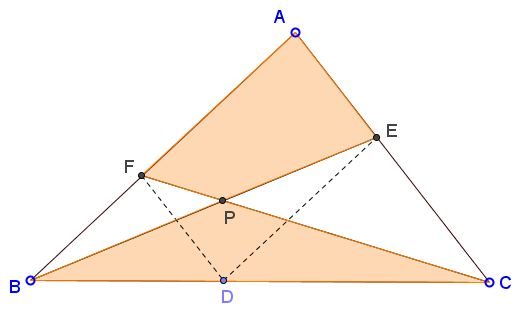
Carpets in Triangle, II - problem

Prove that

$[AEPF] = [BCP],$

where the brackets are used to denote the area of the included shape.

Solution 1

Let $x=BD/BC.\space$ Then $BF =x AB,\space$ $[BFC]=x[ABC]\space$ and $AE=xAC,\space$ $[ABE]= x[ABC].\space$ It follows that $[BFC ]=[ABE]\space$ and, consequently,

$[BFC]-[BFP]=[ABE]-[BFP],$

i.e., $[BPC]=[FAEP].$

(Obviously, the derivation could have been shortened with a reference to the Carpet Theorem.)

Solution 2

This solution depends on the following (stated without proof)

Lemma

In $\Delta MNP,$ lines parallel to the sides are drawn through $Q\in MP.$ $h_1$ and $h_2$ are the heights of their intersection with the corresponding sides, $h$ the altitude from $N.$

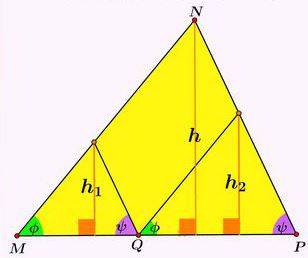
Carpets in Triangle, II - lemma

Prove that $h=h_{1}+h_{2}.$

The lemma applies to the following diagram where $x$, $y$, $m,$ $n$ denote the areas of the enclosing figures. In particular, we need to establish the equality $x=y.$

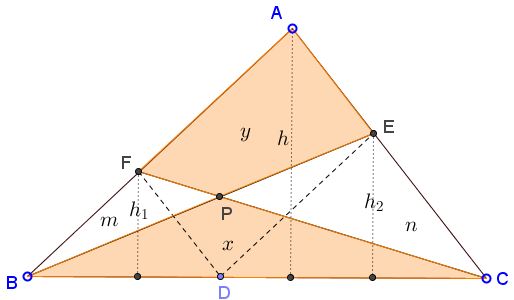
Carpets in Triangle, II - solution

Using the standard fact that "the area of a triangle is half the product of the base times the altitude" derive

$\displaystyle\frac{m+x}{h_1}=\frac{x+n}{h_2}=\frac{m+y+n+x}{h}$

and, as a consequence,

$\displaystyle\frac{m+2x+n}{h_1+h_2}=\frac{m+y+n+x}{h},$

from which (by Lemma) $m+2x+n=m+y+n+x$ and $x=y,$ as required.

Solution 3

The solution is based on the following lemma that is stated here without proof

Lemma

In a trapezoid, the two of the four triangles cut off by the diagonals, namely those adjacent to the sides, have equal areas:

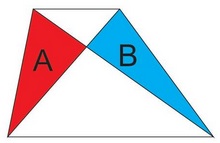
Carpets in Triangle, II - solution #3, Lemma

A=B.

For a proof, observe that there are two trapezoids: $ABDE$ and $AFDC$ to which we apply the lemma:

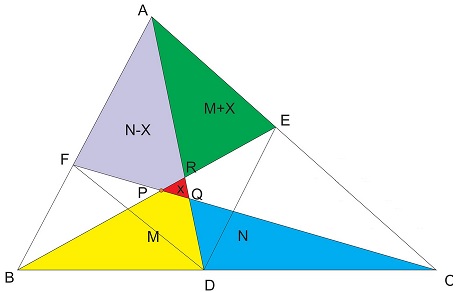
Carpets in Triangle, II - solution #3

The diagram shows that

$[AEPF]=(N-X)+(M+X)=N+M=[BCP],$

as required.

Acknowledgment

The problem by Miguel Ochoa Sanchez has been posted at the Short Mathematical Idea facebook page in the beautiful translation by Leo Giugiuc. Solution 1 is due to Gheorghe Duca, Solution 2 is to Miguel Ochoa Sanchez, Solution 3 is by Ruben Dario.

Carpets Theorem

71873072