The Carpets Theorem With Parallelograms: What is it about?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

In the applet, point M is located on the diagonal BD of the parallelogram ABCD. MN and MP are drawn parellel to the sides of the parallelogram so that another parallelogram - MNCP - is formed. The applet purports to illustrate a simple fact that the combined area of the blue triangles equals that of the red triangle. To see that, we need only use a property of the trapezoids twice. In two trapezoids - ABNM and ADPM - the areas of the triangles formed by the diagonals and adjacent to the nonparallel sides are equal.

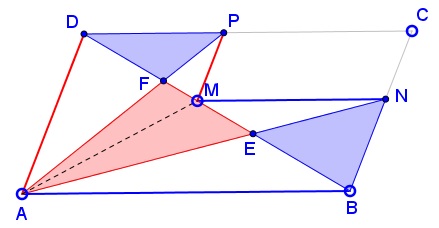
In the applet, the point M is always located on the diagonal BD. But as the proof shows this is not necessary. It may be either in ΔABD or ΔBCD. In one case the red quadrilateral AEMF is a dart, in the other a kite. With M on BD, it's a triangle. In this case we also have a nice application of the Carpets Theorem. We may take as one carpet ΔABD and as the second carpet the union of triangles ABN and ADP. Since both have areas equal to Area(ABCD)/2, the theorem applies immediately. However, the fact is more obvious for ΔABD than for ΔABN ΔADP.

Draw the diagonal AC.

(The latter identity follows from the similarity of triangles BCD and BNM.)

Similarly,

Since Area(ABC) = Area(ACD) = ½Area(ABCD), we get the required result by adding (1) and (2):

References

1. T. Andreescu, B. Enescu, Mathematical Olympiad Treasures, Birkhäuser, 2004

Carpets Theorem

• The Carpets Theorem
• Carpets in a Parallelogram
• Carpets in a Quadrilateral
• Carpets in a Quadrilateral II
• Square Root of 2 is Irrational
• Carpets Theorem With Parallelograms
• Two Rectangles in a Rectangle
• Bisection of Yin and Yang
• Carpets in Hexagon
• Round Carpets
• A Property of Semicircles

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|