Two Rectangles in a Rectangle

In the applet, ABCD, EFGH, and IFJH are all rectangles. Show that

the total of red areas equals the blue area.
the sum of the areas of EFGH and IFJH equals that of ABCD.

Since the diagonals of a rectangle (and even those of a parallelogram) meet at the common midpoint and since the two internal rectangles share one diagonal FH, their diagonals are equal and centers coincide. This point O is also the center of ABCD. Indeed, being the midpoint of FH it lies on the horizontal axis of ABCD. Being the midpoint of, say, EG, it lies on the vertical axis of ABCD.

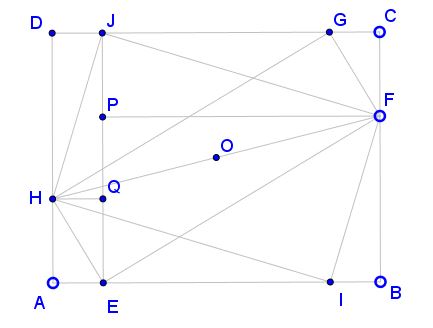
Two rectangles in a rectangle

We found that EG = IG and both pass through the center of ABCD. Hence, triangle GOJ is isosceles and CG = DJ. But then

CG = BI,

such that BCGI is another rectangle and AIGD ie yet another one.

Obviously, Area(IFG) = Area(BCGI)/2 and Area(IGH) = Area(AIGD)/2. It follows that the area of the quadrilateral IFGH is half that of ABCD. The same of course is true for the quadrilateral EFJH:

Area(IFGH) = Area(EFJH) = Area(ABCD)/2.

We are in the framework of a variant of the Carpets Theorem. With IFGH = S₁ and EFJH = T₁ we get the first result: the total of the red areas (uncheck the Hint box) equals that of the blue.

The second result is an immediate consequence of the first.

References

J. Konhauser, D. Velleman, S. Wagon, Which Way Did the Bicycle Go?, MAA, 1996, #52

Carpets Theorem

71534208