Carpets in Triangle
What Might This Be About?
1 March 2014, Created with GeoGebra
Problem
Let $M$ be a point in the interior $\Delta ABC.$ Three lines are drawn through $M$ parallel to the sides of the triangle, thereby producing three trapezoids. With a reference to the diagram below, in each of the trapezoids choose a diagonal so that the three have no common points: $AA',$ $BB',$ $CC'.$ These diagonals divide $\Delta ABC$ into seven pieces of which four are triangles.
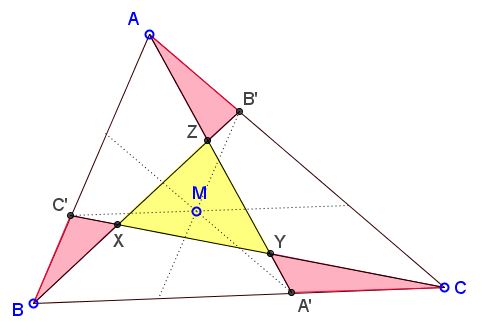
Prove that the area of the central triangle equals the sum of the areas of the other three. More accurately,
$[XYZ] = [AB'Z] = [BC'X] + [CA'Y],$
where the brackets are used to denote the area of the included shape.
Solution
The three triangles $ABB',$ $BCC',$ $CAA'$ cover a certain area, that excludes $\Delta XYZ,$ but with triangles $AB'Z,$ $BC'X,$ $CA'Y$ covered twice.

Due to Euclid I.37, their total area is exactly $[ABC]:$
$[ABB'] + [BCC'] + [CAA'] = [ABM] + [BCM] + [CAM] = [ABC].$
Motivated by the Carpet Theorem, we observe that the area of their overlap equals the uncovered area.
Acknowledgment
This is one of the problems from the most wonderful book by T. Andreescu and B. Enescu. This is actually where I first came across the Carpet Theorem.
References
- T. Andreescu, B. Enescu, Mathematical Olympiad Treasures, Birkhäuser, 2004
Carpets Theorem
- The Carpets Theorem
- Carpets in a Parallelogram
- Carpets in a Quadrilateral
- Carpets in a Quadrilateral II
- Square Root of 2 is Irrational
- Carpets Theorem With Parallelograms
- Two Rectangles in a Rectangle
- Bisection of Yin and Yang
- Carpets in Hexagon
- Round Carpets
- A Property of Semicircles
- Carpets in Triangle
- Carpets in Triangle, II
- Carpets in Right Triangle
- Piecewise Carpets in Parallelogram
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579691
