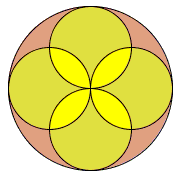
In the diagram below, which areas are bigger - the yellow 'almonds' or the pink 'umbrellas'?
Solution
We shall apply the Carpets Theorem
Assume shape U is split in two ways
U = S1 ∪ S2 = T1 ∪ T2,
such that Area(T1) = Area(S2). Then
Area(S1 ∩ T1) = Area(S2 ∩ T2).
Imagine the big circle U split in two ways as shown:
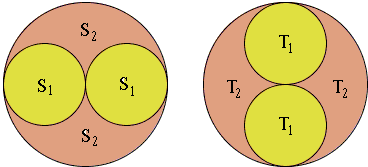
(I assume that, say, S1 is the union of two circles, and similarly T1.)
Since the area of a circle of radius ρ equals πρ², Area(T1) = Area(S1) = ½Area(U). Therefore, also Area(T1) = Area(S2). By the Carpets theorem,
Area(S1 ∩ T1) = Area(S2 ∩ T2),
which is to say that the yellow almonds have the same area as the pink umbrellas.
Note: In general, the Carpets Theorem just claims the obvious fact that if shifting (or placing) a piece of a carpet creates an overlap with another piece then the area of the floor uncovered (not covered) due to the shift (placement) equals the area of the overlap. The theorem applies because the areas of the four small circles add up to the area of the big one. So what they fail to cover needs to be equal to what they cover redundantly. (I thank John Golden for reminding me of this simple interpretation.)
Carpets Theorem
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
