Carpets in Hexagon
Each of the three diagonals of a convex hexagon that join the opposite pair of vertices split the hexagon into polygons of equal area. Prove that the three diagonals meet in a point.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyEach of the three diagonals of a convex hexagon that join the opposite pair of vertices split the hexagon into polygons of equal area. Prove that the three diagonals meet in a point.

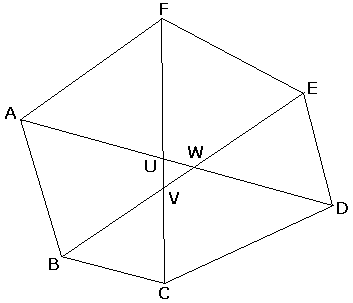
Assume to the contrary that the diagonals do not concur but, instead, form a triangle, as in the diagram.
Considering two diagonals at a time, we may apply the Carpets Theorem three times. Say, for diagonals AD and BE, we have that the areas of quadrilaterals BCDW and AWEF are equal as are the areas of triangles ABW and DEW. We focus on the areas of the triangles. With other pairs of diagonals, we obtain two additional area identities. To summarize,
Area(BCV) = Area(EFV),
Area(CDU) = Area(FAU).
The area of a triangle can be found as half the product of any two sides and the sine of the angle between the two side. With this in mind, the above three identities imply the following
EV × FV = BV × CV,
CU × DU = FU × AU.
Let's multiply the three:
But this is impossible because every term on the left is greater than the corresponding term on the right. The diagonal then are bound to concur.
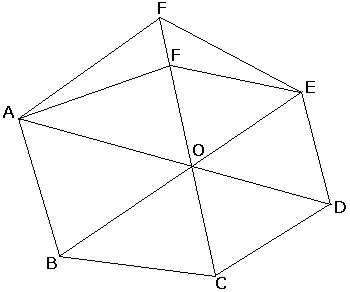
The condition that the three diagonals are the area splitters is sufficient for the concurrence of the diagonals. The converse is rather obviously not true: the condition is not necessary. If in the hexagon ABCDEF the diagonal CF splits the area then moving one of the vertices, say F, along the diagonal CF will not disturb the concurrence of the diagonals but will decimate the equality of areas: the area of BCDO remains the same while the area of its counterpart AOEF changes.
Carpets Theorem
- The Carpets Theorem
- Carpets in a Parallelogram
- Carpets in a Quadrilateral
- Carpets in a Quadrilateral II
- Square Root of 2 is Irrational
- Carpets Theorem With Parallelograms
- Two Rectangles in a Rectangle
- Bisection of Yin and Yang
- Carpets in Hexagon
- Round Carpets
- A Property of Semicircles
- Carpets in Triangle
- Carpets in Triangle, II
- Carpets in Right Triangle
- Piecewise Carpets in Parallelogram
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581124
