Piecewise Carpets in Parallelogram
What Is This About?
Problem
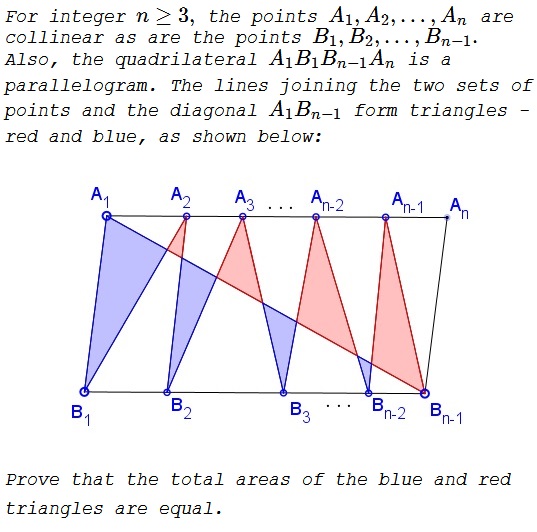
Solution 1
Consider two partitions of the parallelogram: $T_1\cup T_2$ and $S_1\cup S_2,$ where $T_1=\Delta A_1B_{n-1}A_{n},$ $T_2=\Delta A_1B_1B_{n-1},$ $\displaystyle S_1=\bigcup_{i=1}^{n-2}\Delta B_iA_{i+1}B_{i+1}$ and $\displaystyle S_2=\bigcup_{i=1}^{n-1}\Delta A_iB_{i}A_{i+1}:$
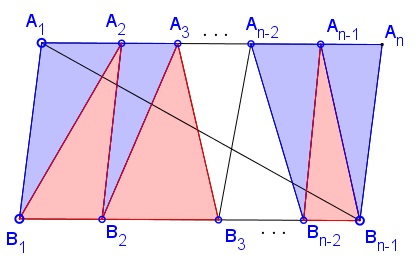
Obviously, $[T_1]=[T_2]=[S_1]=[S_2].$ It follows from the Carpets Theorem that $[T_1\cap S_1]=[T_2\cap S_2].$ This is exactly the required identity.
Solution 2
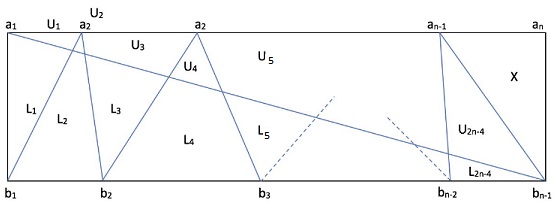
Area above the diagonal equals the area below the diagonal:
$\displaystyle\begin{align}&\sum_{\text{all }i}U_i+X=\sum_{\text{all }i}L_i\\ &\sum_{\text{odd }i}U_i+\sum_{\text{even }i}U_i+X=\sum_{\text{odd }i}L_i+\sum_{\text{even }i}L_i. \end{align}$
Or, to introduce some notations,
$U_{odd}+U_{even}+X=L_{odd}+L_{even}.$
The area of the triangles with the base on top equals the area of the triangles with the base below:
$\displaystyle\begin{align}&\sum_{\text{even }i}(L_i+U_i)=\sum_{\text{odd }i}(L_i+U_i)+X\\ &\sum_{\text{even }i}L_i+\sum_{\text{even }i}U_i=\sum_{\text{odd }i}L_i+\sum_{\text{odd }i}U_i+X. \end{align}$
With similar notations: $L_{even}+U_{even}=L_{odd}+U_{odd}+X.$ Summing up the expressions for the areas,
$U_{odd}+L_{even}+2U_{even}+X=2L_{odd}+L_{even}+U_{odd}+X,$
which, after canceling similar terms, reduces to $2U_{even}=2L_{odd}.$
Acknowledgment
This is a generalization of problem 5465 from the MATHPROBLEMS JOURNAL. The original problem was by Arsalan Wares (Valdosta State University, Valdosta, GA):

Solution 2 is by Daniel P.
Carpets Theorem
- The Carpets Theorem
- Carpets in a Parallelogram
- Carpets in a Quadrilateral
- Carpets in a Quadrilateral II
- Square Root of 2 is Irrational
- Carpets Theorem With Parallelograms
- Two Rectangles in a Rectangle
- Bisection of Yin and Yang
- Carpets in Hexagon
- Round Carpets
- A Property of Semicircles
- Carpets in Triangle
- Carpets in Triangle, II
- Carpets in Right Triangle
- Piecewise Carpets in Parallelogram
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73558850
