Midpoints of the Lines Joining In- and Excenters
What is this about?
A Mathematical Droodle
Discussion
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
The applet suggests that the midpoints of the lines joining the incenter of a triangle with its excenters all lie on the circumcircle of the triangle. Why this is so?
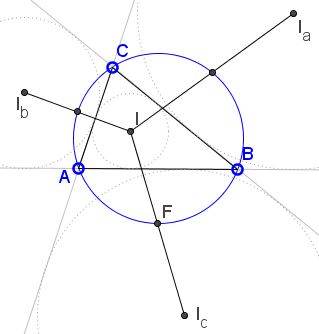
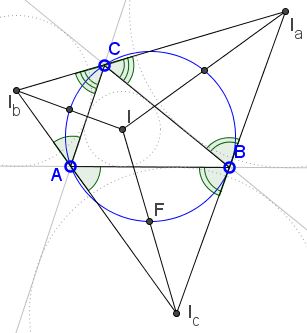
At every vertex of the triangle the bisectors of the internal and external angles are two perpendicular lines. The lines joining the excenters are none other than the bisectors of the external angles and thus pass through the vertices of the given triangle. Let the triangle be ABC, the excenters Ia, Ib, Ic and the incenter I. Because of the preceding remark, the angle bisectors of DABC play the role of the altitudes in DIaIbIc. This exactly means that the DABC is orthic with respect to DIaIbIc. (We arrive at the same conclusion noticing that DABC has the mirror property in DIaIbIc.) It follows that the circumcircle of DABC is also the 9-point circle of DIaIbIc.
The 9-points that make its name are the three feet of the altitudes, the midpoints of the sides and the three Euler points: the midpoints of the segments from the orthocenter to the vertices. In our case, these are exactly the midpoints of IIa, etc.
In passing, DIaIbIc is known as the excentral triangle of DABC. As we just saw, a triangle is the orthic triangle of its excentral triangle. Its incenter, serves as the orthocenter of the latter.
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
| 
