Paper Folding Geometry

Origami is an ancient Chinese and Japanese art of paper folding. From the Brief History of the Ancient Art of Paperfolding I gather that Origami gained acceptance in the West in the early 1950s. Very comprehensive bibliographies are available online. A search of the online bookstore has resulted in several dozen books and albums. In my own library, I discovered several books wholly or in part devoted to the mathematics of paper folding (see bibliography below.) Unexpectedly, information available online proved to be scarce. (This may explain an unexpected reference to my logo page.) Following is my attempt to catch up with the development of the last 50 years of which, regretfully, I knew so little. My main source of information was a collection of pages put together by Tom Hull of Merrimack College.

In the geometry of paper folding, a straight line becomes a crease or a fold. Instead of drawing straight lines, one folds a piece of paper and flattens the crease. Folding paper is analogous to mirroring one half of a plane in a crease. Thus folding means both drawing a crease and mapping one half of a plane onto another. As in the usual Geometry, the distinction is being made between experimentation with the physical paper and the abstract theory of "paper folding". "Abstract paper" may be folded indefinitely although in practice the number of folds is by necessity limited.

In the Paper Folding Geometry, a straight line - a fold - is clearly a primary object; a point is defined as the intersection of two folds. But why a fold can be thought of as modeling a straight line? This question was posted as a problem in the American Mathematical Monthly in 1939 and answered in 1940 (E395, p. 398):

In high school geometry texts and elsewhere one frequently meets the statement that the reason for straightness of a crease in a folded piece of paper is that the intersection of two planes is a straight line. This is fallacious. What is the correct reason?

The answer is

Let P, P' be two points of the paper that are brought into coincidence by the process of folding. Then any point A of the crease is equidistant from P, P', since the lines AP, AP' are pressed into coincidence. Hence the crease, being the locus of such points A, is the perpendicular bisector of PP'.

To put it candidly, I am not sure why the reference to the intersection of two planes is fallacious. Perhaps, because the argument would require an additional assumption of a paper piece being a plane figure. However, it seems to me that the "correct" argument assumes at least as much. Perpendicular bisectors exist in geometries other than the Euclidean plane, e.g., they are naturally defined on a sphere.

It's not an idle question. In essence, it's a question of the relationship between mathematics and the worldly experience. Here is a later day answer to the same question (D. Fuchs, S. Tabachnikov, More on Paperfolding, The Am Math Monthly, v 106, n 1, 1999, 27-35).

It's a common knowledge that folding a sheet of paper yields a straight line. We start our discussion of paper folding with a mathematical explanation of this phenomenon. The model for a paper sheet is a piece of the plane; folding is an isometry of the part of the plane on one side of the fold to another, the fold being the curve of fixed points of this isometry. The Statement is that this curve is straight, that is, has zero curvature.

If not, consider an arc γ of the fold with nonvanishing curvature. Let γ⁺ be a curve at (small) distance ε from γ on the concave side, and let γ⁻ be the corresponding curve on the convex side.

Then

length γ⁺ > length γ > length γ⁻ ,

where the difference between length γ⁺ and γ⁻ is of order

ε · length γ · curvature γ.

On the other hand, the isometry takes γ⁺ to γ⁻ , so

length γ⁺ = length γ⁻ .

This is a contradiction.

Pretty curiously the next sentence in the paper reads: In spite of what has just been said, one can fold paper along an arbitrary smooth curve! All it takes to accomplish this feat is to give up the requirement that the portions of the paper on two sides of the curve meet at zero angle. This requirement is implicit in the "flattening out" operation applied to a crease in paper folding geometry.

As opposed to origami by which I mean a practical art of creating paper artifacts, paper folding as a mathematical discipline of geometric construction was introduced in 1983 by T. Sundar Row and first put on a rigorous basis by R. C. Yates in 1949. Yates listed three axioms: O1, O2 and O5 below. Yates showed that all plane Euclidean constructions can be based on these three.

In 1991, the Italian-Japanese mathematician Humiaki Huzita formulated 6 axioms of paper folding each abstracting an operation feasible with a concrete piece of paper. I shall describe the axioms in terms of the construction with the straightedge and compass. (For another write-up see Wikipedia.) He has shown that angle trisection can be performed for any angle defined by two folds.

	Axiom	Construction
O1	There exists a single fold connecting two distinct points.	This is the first of Euclid's Postulates
O2	Given two points P₁ and P₂, there exists a unique fold that maps P₁ onto P₂.	Draw the perpendicular bisector of P₁P₂: Sweep two arcs with centers at the two points and the same radii. Connect the points of intersection.
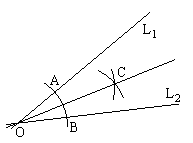
O3	Given two creases L₁ and L₂, there exists a unique fold that maps L₁ onto L₂.	Draw the angle bisector between L₁ and L₂ (If the lines are parallel, this is another parallel line midway between L₁ and L₂): Let O be the point of intersection of L₁ and L₂. From O, along L₁ and L₂ measure equal segments OA and OB. Draw two arcs of equal radii centered at A and B till they intersect at C. OC is the angular bisector of the angle defined by L₁ and L₂ in case they intersect.
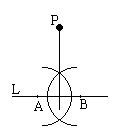
O4	Given a point P and a crease L, there exists a unique fold through P perpendicular to L.	Drop a perpendicular from a point to a line: Find two points A and B on L equidistant to P. With centers at A and B, draw two arcs of equal radii till their intersection. Each of the cross points lies on the sought perpendicular.
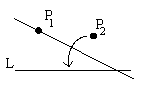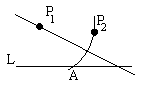
O5	For given points P₁ and P₂ and a crease L, there exists a fold that passes through P₁ and maps P₂ into L.	With radius P₁P₂ and center P₁, draw an arc till it intersects L at point A. Drop a perpendicular from P₁ on AP₂ (Axiom O4). Remark: Obviously the construction is only possible if the length of P₁P₂ is not less than the distance from P₁ to L. Therefore, axiom O5 can't universally hold. I will have to look into the original source for clarification. Even when it exists the fold may not be unique.
O6	Given two points P₁ and P₂ and two creases L₁ and L₂, there exists a unique fold that maps P₁ into L₁ and P₂ into L₂.	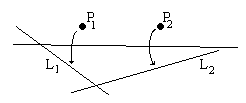As shall be seen, axiom O is equivalent to solving a third degree equation. Therefore, in general, it can't be performed with the straightedge and compass.

One of the simplest and most natural paper folding procedures is to form a flat "paper roll" by folding the paper several times with creases parallel to each other. In this manner, we obtain equidistant points on any crease not parallel to the fold. The paper folding geometry may be expected to justify this construction. Indeed, from axiom O4 we get the following

Statement

Let points P₁ and P₂ lie on a crease L.
There exists a unique point P on L (different from P₁)
such that PP₂ = P₁P₂.

References

P. Hilton and J. Pedersen, Connecting Geometry and Number Theory, in In Eves' Circles, MAA, 1994
P. Hilton and J. Pedersen, Build Your Own Polyhedra, Addison-Wesley, 1994
P. Hilton, D. Holton, J. Pedersen, Mathematical Reflections, Springer, 1997
G. E. Martin, Geometric Constructions, Springer, 1998
M. Senechal and G. Fleck (eds), Shaping Space, Birkhaüser, 1988

Paper Folding Geometry

72104867