Menelaus from 3D

Invocation of 3D imagery often serves a powerful tool in proving theorems of plane geometry. Farther down the page there are links to several demonstrations of this idea. On November 28, 2010, Hubert Shutrick had a vision that rendered a one-liner proof of Menelaus' theorem.

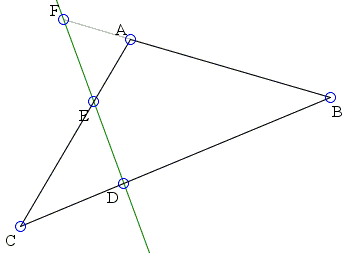
Menelaus' theorem

Let three points F, D, and E, lie respectively on the sides AB, BC, and AC of ΔABC or their extensions. Assume just one or all three of the points lie on side extensions. Then the points are collinear iff

AF

BF
·
BD

CD
·
CE

AE
= 1

Proof (Hubert Shutrick)

Put up a flagpole AA' orthogonal to the plane and let B' and C' be the points where the orthogonal lines through B and C meet the plane A'DEF. If the heights of the verticals are h_a, h_b and h_c, possibly negative, then similar vertical right triangles give

h_a/h_b = AF/BF, h_b/h_c = BD/CD and h_c/h_a = CE/AE

which, when multiplied together, produce exactly the required identity.

Conversely, assume Menelaus' identity holds. Erect AA' and consider the plane A'EF. Define B' and C' as before, and D' the intersection of B'C' with BC. Then

h_a/h_b = AF/BF, h_b/h_c = BD'/CD' and h_c/h_a = CE/AE.

Comparing the product of the three with Menelaus' identity shows that BD'/CD' = BD/CD, implying D = D' and, subsequently, the collinearity of D with E and F.

2D Problems That Benefit from a 3D Outlook

Menelaus and Ceva

71924403