A Property of Equiangular Polygons
What Is It About?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
(Note: the side lines of the depicted polygon which is initially regular can be dragged. The side lines always remain parallel to their original position. The operation therefore affects the side lengths but preserves the angles of the polygon. The result is an equiangular polygon, i.e., a polygon with equal angles. This is at least true as long as the polygon remain simple, or, which in this case is the same, convex.)
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
A Property of Equiangular Polygons
The applet suggests a generalization of Viviani's theorem:
The sum of distances from a point to the side lines of an equiangular polygon does not depend on the point and is that polygon's invariant.
An equilateral triangle is also equiangular (by SSS), and vice versa. The two properties do not necessarily come together if the number of sides (and, therefore, angles) exceeds 3. A polygon which is both equiangular and equilateral is regular. Viviani's theorem is easily extended to regular and, in fact, equilateral polygons. The proof is simple: connect a point to the vertices of the polygon to obtain a series of triangles with the apex at the given point and the base on a side of the given polygon. Let hi be the (signed) distance from the given point to side #i. If the common side length is denoted a, the area of the polygon will be given as
| (1) | Σahi/2 = (a/2)Σhi. |
(Here the area ahi/2 is positive if the orientations of the triangle #i and the polygon coincide and is negative otherwise.) Since neither S nor a/2 depend on point selection, Σhi is also independent of the point.
It's less obvious that the property claimed by Viviani's theorem is also carried over to the equiangular polygons.
| Buy this applet What if applet does not run? |
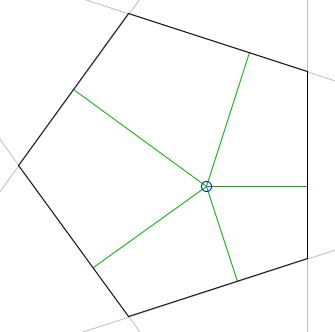
The proof is simple and elegant. Quite obviously, an equiangular polygon can be embedded into a regular polygon with parallel sides. This can be done in a continuum of ways. But fix a suitable regular polygon, so that the distances between the corresponding sides of the two polygons remain constant. Then clearly if (1) holds for one of them, it also holds for the other. We have just seen that it does hold for regular polygons, so it holds for the equiangular ones.
A converse is true for triangles: if the sum of distances from a point to the sides of a triangle is independent of the point, the triangle is equilateral. To see this, place the point at the vertices of the triangle. We then have that in the triangle all three altitudes coincide. From S = ah/2 (for a triangle) we conclude that the sides are also equal.
The converse does not hold for other polygons. Even for a quadrilateral, parallelogram serves as a counterexample.
Michel Cabart offered a different approach. (This is an extention of a proof without words of Viviani's theorem by Hans Samelson). Let A be a point inside the polygon, ni unit vectors perpendicular to the ith of the polygon, and Hi the feet of the perpendicular from A to the ith side. Since the polygon is equiangular, the angles between successive vectors ni are equal, so that
The sum of distances from A to the sides of the polygon is
SA = ΣAHi = Σ(AHi, ni).
For another point B with pedals Gi the distance is
SB = ΣBGi = Σ(BGi, ni) = Σ(BHi, ni).
So that
SA - SB = (AB, Σni) = 0.
References
- T. Andreescu, B. Enescu, Mathematical Olympiad Treasures, Birkhäuser, 2004
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
| 49552214 |
