Scott E. Brodie

We take the Parallel Postulate in the form known as Playfair’s Axiom:

This axiom, or its equivalent, seems to be necessary to prove the Pythagorean Theorem:

The proofs of the Pythagorean Theorem seem to divide into three main types: proofs by shearing, which depend on theorems that the areas of parallelograms (or triangles) on equal bases with equal heights are equal, proofs by similarity, which depend on calculations of proportions of sides of similar triangles, and proofs by dissection, which depend on the observation that the acute angles of a right triangle are complementary. In each case, the argument can readily be traced back to consequences of the Parallel Postulate. In this sense, in the presence of the remainder of the axioms for plane geometry, we observe that I implies II.

Many of the consequences of the Parallel Postulate, taken together with the remainder of the axioms for plane geometry, can be shown in turn to imply the Parallel Postulate. In this sense, these statements can be regarded as equivalent to the Parallel Postulate. They include such well-known theorems as

• VI implies VII
• VII implies VIII
• VIII implies IX
• IX implies I

On these pages, we add to this list the observation that

As we have already observed that I implies II, we thus establish that the Pythagorean Theorem itself is yet another proposition which may be taken as an equivalent alternative to the Parallel Postulate.

In proving these implications, we must be careful to use only those theorems that can be deduced without the use of the Parallel Postulate. In particular, we may copy known segments and angles, and apply the triangle congruence theorems, and we may employ the exterior angle theorem. We must avoid calculations of areas and the usual theorems about parallel lines (such as III, IV, and V) and similarity.

II implies VIII

Actually, we prove the slightly stronger statement:

Let ABC be any right triangle, with right angle C. Draw the altitude CF from the right angle to the hypotenuse. As usual, a, b, c are the sides opposite vertices A, B, C. Let x = BF, y = FA, and h = CF. Then BFC and CFA, as well as BCA are right triangles, and we may apply the Pythagorean assumption three times:

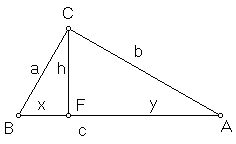
a² + b² = c²

x² + h² = a²

h² + y² = b²

c² = (x + y)² = x² + y² + 2xy

Substituting the last three equations into the first we obtain

x² + h² + h² + y² = x² + y² + 2xy, or

2h² = 2xy, and

h/x = y/h.

Set this common ratio h/x = y/h = k. Then h = kx, y = kh, and we have

b² = h² + y² = k²(x² + h²) = k²a², so

b/a = k = h/x = y/h.

Similarly, we may show that

b/c = h/a = y/b,

Thus the corresponding sides of the two small triangles are proportional, as are the corresponding sides of the original triangle and either of the small triangles.

It would be tempting to conclude that, since the corresponding sides of the triangles are proportional, the corresponding angles are equal. This implication, however, is a consequence of the Parallel Postulate, and does not hold in general. However, in the special case of an isosceles right triangle, we may proceed as follows:

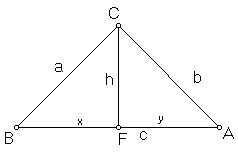
Since a = b, and since a/b = x/h, we have x = h; similarly, h = y. Thus triangles BFC and AFC are likewise isosceles, and their base angles FBC, BCF, FCA, and FAC are all equal. Since angles BFC and CFA are right, we conclude that triangles BFC and CFA are equiangular with each other, and with triangle ACB.

But angle BCF and angle FCA sum to one right angle. Therefore, the equal angles FBC and FAC sum to one right angle, and the angles of the original triangle sum to two right angles.

Legendre’s theorems:

Lemma 1

In a triangle, the sum of any two angles must be less than two right angles.

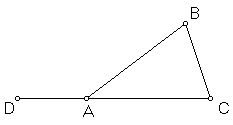
In ΔABC, consider the sum of angles CAB and ABC. Consider the exterior angle DAB adjacent to angle CAB. The sum of angles DAB and CAB is two right angles, as they are supplementary. By the exterior angle theorem, angle ABC, being a remote interior angle, is less than angle DAB. Therefore, the sum of the two (interior) angles CAB and ABC must be less than two right angles.

Lemma 2

In any triangle, the sum of the three angles is less than or equal to two right angles.

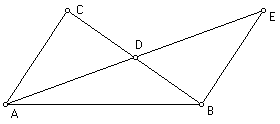
In ΔABC, suppose the sum of the three angles ABC, BCA, CAB exceeds to right angles by an amount, a. Suppose the labeling such that &nag;ABC £ &nag;BCA, and bisect CB at D. Extend AD to E such that AD = DE. Then ΔCAD = ΔBED. In particular, &nag;ACD = &nag;EBD, and &nag;CAD = &nag;BED. Thus, the sum of the three angles of ΔABC equals the sum of the three angles of ΔABE.

Now, since &nag;ABC £ &nag;BCA, AC £ AB, hence EB £ AB. Thus &nag;EAB £ &nag;AEB. But &nag;BAC = &nag;EAB + &nag;DAC = &nag;EAB + &nag;AEB. It follows that &nag;EAB £ ½ &nag;CAB. Thus, we have constructed a triangle, ABE, whose three angles sum to the same total as our original ΔABC, but with one angle at most half one of the angles in the original triangle.

This process can be repeated as many times as necessary, until we obtain a triangle one of whose angles is less than a, the excess of the original angle sum over two right angles, and whose total angle sum is the same as that of the original triangle. But then the sum of the two remaining angles must exceed two right angles, which contradicts Lemma 1.

Therefore, the angle sum of the original triangle cannot exceed two right angles.

Let the angles of the first subsidiary triangle sum to S1, and those of the second to S2. Then the angles of the original triangle sum to S1 + S2 less two right angles. If S1 is less than two right angles, then S2 must be greater than two right angles, in order that the sum equal two right angles. But this would contradict Lemma 2.

VI implies VII

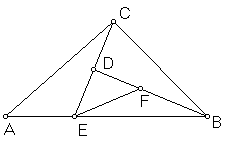
If there exists one triangle whose angle sum equals two right angles, then there exists an isosceles right triangle whose angle sum equals two right angles.

In ΔABC, whose angle sum is two right angles, let BC be the shortest side. Choose E on AB so that EB = BC. Draw CE; then by Lemma 3, the angle sum of ΔBCE is two right angles. Draw median BD. Then ΔBDE is right, and its angle sum is two right angles. If DEDB, pick F on DB so that DF = DE. Then ΔDFE is a right isosceles triangle whose angle sum equals two right angles. If DE > DB, pick F on DE so that DF = DB; then ΔDFB is again as required.

VII implies VIII

If there exists an isosceles right triangle whose angles sum to two right angles, then there exists an arbitrarily large isosceles right triangle whose angles sum to two right angles.

Placing two copies of the isosceles right triangle with angle sums equal to two right angles together, hypotenuse to hypotenuse, yields a quadrilateral with four equal sides and four right angles. Placing four such squares together yields a square whose sides are twice as large. Repeating this process as needed, we obtain a square whose side exceeds any specified length. Either diagonal divides this square into two isosceles right triangles whose angle sum is two right angles, as required.

VIII implies IX

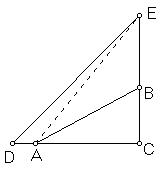If the angles of an arbitrarily large isosceles right triangle sum to two right angles, then the angles of every right triangle sum to two right angles.

Let ΔABC be right, with right angle at C. Then the legs can be extended to D and E respectively so that ΔDCE is an isosceles right triangle whose three angles sum to two right angles. Then we may apply Lemma 3 to conclude that the angle sum of the ΔEAC is equal to two right angles, and then again to conclude that the angle sum of ΔABC is equal to two right angles.

Corollary

If any of VI, VII, or VIII hold, than the sum of the three angles of any triangle is equal to two right angles.

Any triangle can be divided in the manner of Lemma 3 into two right triangles.

Lemma 4

Given a line and a point not on it, a line may be drawn through the point, intersecting the line so that the angle formed is less than any pre-assigned angle.

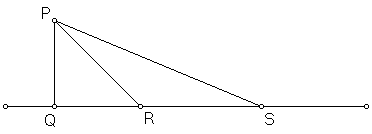
Draw the perpendicular PQ from the point P to the line; choose R on the line so that PQ = QR. Draw PR, and choose S on the line (with R between Q and S) so that PR = RS. Then since &nag;QRP plus &nag;PRS equals two right angles, but (by Lemma 2), the sum of angles PRS, RPS, and RSP is at most two right angles, it follows that the sum of angles RPS and RSP is at most equal to &nag;PRQ. Since ΔRPS is isosceles, angles RPS and RSP are equal, and therefore each is at most ½&nag;PRQ.

Repeating the construction as necessary, we obtain an angle less than any pre-assigned magnitude.

IX implies I

If the three angles of any right triangle sum to two right angles, then through a given point, only one line can be drawn parallel to a given line.

Draw the perpendicular PQ from the point P to the given line l. Construct the line r through P, perpendicular to PQ. Then r is parallel (that is, doesn’t intersect) with line l, for a triangle with two right angles contradicts Lemma 1. Suppose there is another line s through P parallel to l. Since s is distinct from r, we may choose a point T on s such that angle TPQ is less than a right angle. Denote the difference by a.

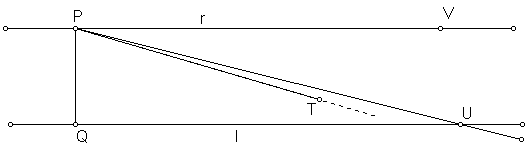
Now use Lemma 4 to construct a line through P, intersecting l at U, such that angle PUQ is less than a. Let V be a point of r on the same side of PQ as U.

Then, since &nag;PQU is right, the angles of ΔPQU sum to two right angles, and the sum of angles QUP and QPU is a single right angle. But &nag;QPV, the sum of angles QPU and UPV, is likewise right. It follows that angles QUP and UPV are equal. This means that angle UPV is less than a. Since &nag;TPV equals a, the ray PT must lie in the interior of &nag;QPU, and must therefore necessarily intersect line l (somewhere between Q and U). This contradicts the supposition that line s is parallel to line l, and we conclude that the parallel r through P is unique.

Remark

It should not be surprising that the Pythagorean Theorem implies the Parallel Postulate, as the Pythagorean Theorem serves as the starting point for at least two different alternative approaches to the "synthetic geometry" used here:

In "analytic geometry", the Pythagorean Theorem appears as the "distance formula" between points. In that context, the Parallel Postulate emerges as a paraphrase of the algebraic conditions for two simultaneous linear equations to have no solution, as opposed to either a single solution, or an infinite set of solutions.

In "differential geometry", advanced calculus is used to describe measurements made within a curved surface. In this context, the Pythagorean Theorem appears as one possible formula (among many) for the length of a curve. If this formula for the length of a curve is chosen, the "curvature" (technically, the "Gaussian curvature") achieves the value of zero, and the classical result that the angles of a triangle sum to two right angles follows from the famous "Gauss-Bonnet Theorem".

References:

1. Heath, T, Euclid's Elements, Volume I, pp 202-220, Dover Publications, NY
2. Hilbert, D, Foundations of Geometry, 10th Edition, Open Court, LaSalle, IL, 1971

David Henderson, mathematics professor at Yale and author of a stunning book Experiencing Geometry (Prentice Hall, 2004), remarked that Playfair's axiom is not quite equivalent to Euclid's Fifth Postulate.

If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.

Indeed, Euclid's postulate trivially holds on sphere, because any two "straight" lines on sphere intersect. Playfair's postulate, for the very same reason, trivially does not hold on sphere. In the plane, of course, each implies the other.

• Non-Euclidean Geometries, Introduction
• The Fifth Postulate
• The Fifth Postulate is Equivalent to the Pythagorean Theorem
• The Fifth Postulate, Attempts to Prove.
• Similarity and the Parallel Postulate
• Non-Euclidean Geometries, Drama of the Discovery.
• Non-Euclidean Geometries, As Good As Might Be.
• The Many-Faced Geometry
• The Exterior Angle Theorem - an appreciation
• Angles in Triangle Add to 180^o

Copyright © 1996-2009 Alexander Bogomolny