Angles in Triangle Add to 180°
It's an oft repeated point that Euclid in his Elements has postponed invoking the Fifth Postulate till Proposition I.29:
| A straight line falling on parallel straight lines makes alternate angles equal to one another, the exterior angle equal to the interior and opposite angle, and the interior angles on the same side equal to two right angles. |
With a reference to the diagram
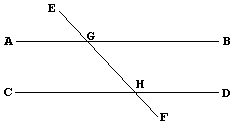
|
the nomenclature is as follows: angles BGH and CHG are alternate; angles BGH and DHG are enterior on the same side; the interior angle DHG is opposite the exterior angle EGB.
The first mention of parallel lines occurs in the Proposition I.27, though. In preparation to I.29, Euclid first proves its converse in I.27 and I.28. I.27 covers one part of I.29:
| If a straight line falling on two straight lines makes alternate angles equal to one another, the straiht lines will be parallel to one another. |
Proposition I.28 supplies the converse for the remaining part of I.29:
| If a straight line falling on two straight lines makes the exterior angle equal to the interior and opposite angle on the same side, or the interior angles on the same side equal to two right angles, the straiht lines will be parallel to one another. |
Note in passing that the converses of I.29 do not require the Fifth Postulate. Both I.27 and I.28 belong therefore to Absolute Geometry.
Proposition I.30 asserts the transitivity of parallelism:
| Straight lines parallel to the same straight line are aslo parallel to one another. |
Proposition I.31 gives a construction of a line through a given point parallel to the given line:
| Through a given point to drawa straight line parallel to a given straight line. |
Proposition I.32 is what really concerns us here:
| In any triangle, if one of the sides be produced, the exterior angle is equal to the two interior and opposite angles, and the three interior angles of the triangle are equal to two right angles. |
Proposition I.32 is among the many equivalent to the Fifth postulate. In addition to Euclid's, the commentary by Sir Thomas Heath lists the proofs by Pythagoras and B. F. Thibaut (1809) which he shows to be circular. He remarks on the ease with which a faulty argument may delude the author. He then gives a second example by Proclus.
Proof 1 (Euclid)
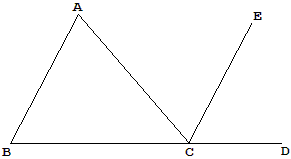
|
Let ABC be a triangle, and let one side of it BC be produced to D. Draw CE parallel to AB (Proposition I.31). Since AB||CE and AC has fallen upon them, the alternate angles BAC and ACE are equal (Proposition I.29). Also by Proposition I.29, since AB||CE and BD has fallen upon them, the exterior angle ECD is equal to the interior and opposite angle ABC. It follows that the exterior angle ACD is equal to the sum of two interior and opposite angles (in triangle ABC) BAC and ABC:
| ∠ACD = ∠CAB + ∠ABC. |
Add on both sides ∠ACB. On the left we get two right angles; on the right the sum of the angles in DABC. Q.E.D.
Proof 2 (The Pythagoreans)
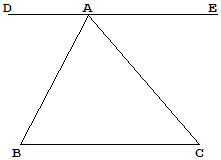
|
The Pythagorean proof is even simpler. A line parallel to the base BC is drawn through the vertex A, which gets us two pairs of alternate angles: CBA, DAB and BCA, EAC. Now, angle BAC complements, on the one hand,
Proof 3 (Thibaut, 1809)
Since the assertion to be proved is equivalent to the Parallel postulate, the proof below should be considered as an attempt to prove the latter.
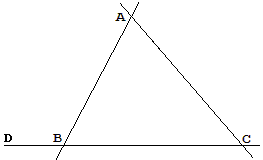
|
(Heath) Suppose CB produced to D, and let BD (produced to any necessary extent either way) revolve in one direction (say clockwise) first about B into the position BA, then about A into the position AC produced both ways, and lastly about C into the position CB produced both ways.
The argument then is that the straight line BD has revolved through the sum of the three exterior angles of the triangle. But, since it has at the end of the revolution assumed a position in the same straight line with the original position, it must have revolved through four right angles.
Therefore the sum of the three exterior angles is equal to four right angles from which it follows that the sum of the three angles of the triangle is equal to two right angles.
Remark
As we now know, something is wrong in Thibaut's argument. But what?
Even on a sphere, where the parallel postulate does not hold and the sum of angles in a triangle need not be 180°, a complete revolution around a point measures four right angles. However, three successive rotations around the vertices of a triangle do not necessarily cause a line to rotate four right angles! To see that, imagine a spherical equilateral triangle with all three angles right.
The fact is that the successive execution of rotations around the vertices of a triangle results in a rotation combined with a translation. The line BC indeed returns to its original position, but not pointwise. It is also shifted along the way. Somewhere in establishing the fact that the resulting rotation equals four right angles the Parallel postulate is bound to crop in.
Proof 4 (Paper Folding)
A proof by paper folding has been placed on a separate page.
References:
- T. Heath, Euclid's Elements, Volume I, pp 307-321, Dover Publications, 1956, NY
- Non-Euclidean Geometries, Introduction
- The Fifth Postulate
- The Fifth Postulate is Equivalent to the Pythagorean Theorem
- The Fifth Postulate, Attempts to Prove.
- Similarity and the Parallel Postulate
- Non-Euclidean Geometries, Drama of the Discovery.
- Non-Euclidean Geometries, As Good As Might Be.
- The Many-Faced Geometry
- The Exterior Angle Theorem - an appreciation
- Angles in Triangle Add to 180°
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73562722
