Sierpinski Gasket and Tower of Hanoi
In the discussion on Sam Loyd's Fifteen puzzle we introduced the notion of puzzle graph. More generally the idea applies to every puzzle, game, or problem (not necessarily mathematical) that may be described by a set of parameters. With every move, parameter values change and the puzzle looks a little different. We are looking into a vector (an ordered set) of parameters whose values uniquely describe appearance (or configuration, or state) of the puzzle. To represent a puzzle graphically, associate various (legitimate) configurations of the puzzle with dots in some space (practically, it's a piece of paper or a computer screen we'll be working with). For every move from one configuration to another, connect the corresponding dots with an edge. If the move is not reversible, the edge must be directed. Otherwise, it's a plain curve connecting the two dots. To solve the puzzle, find dots corresponding to the initial and the target configuration and the path (of moves) from one to the other. If no such path exists the problem is unsolvable.
For a given puzzle G, puz(G) designates the associated puzzle graph. As was discovered by Ian Stewart, puz(Tower of Hanoi) has a surprising relationship to the Sierpinski gasket (also known as the Sierpinski triangle) and, therefore, to Pascal's triangle.
In the Tower of Hanoi puzzle, disks stacked on one peg are to be moved to another with, perhaps an intermediate stop at a third, auxiliary peg. Disks are all of different sizes and it's forbidden to place a bigger disk on top of a smaller one. Number the pegs 1,2, and 3. Every disk may be said to be at one of the pegs and, for a specific configuration, be associated with one of the numbers: 1, 2, 3. A puzzle configuration is completely defined by a list of such peg numbers associated with every disk. To avoid ambiguity the disks are ordered according to their sizes, with the smallest being the first.

For a puzzle with a single disk, only three configurations are possible: (1), (2), (3), where, for example, (2) denotes the configuration in which the lone disk is located at the peg #2. For a puzzle with two disks, there are 9 possible configurations.

As Stewart observed, such pretty configuration can't be coincidence. Let puz(N) denote puz(Tower of Hanoi with N disks). Why puz(2) consists of three copies of puz(1)? Why there is a single edge from one copy of puz(1) to another? The explanation is not only easy, it's also generic: puz(N) always consists of three copies of
Indeed, place the largest disk on one of the three pegs and, for a while, forget about it. The remaining disks form a smaller puzzle. To three possible locations of the largest disk there correspond three "subpuzzles". The largest disk can only be moved with all the smaller ones stacked on a single peg (so that the third peg is free).

Well, the structure suspiciously resembles two famous triangles: Pascal's and Sierpinski's. We've seen by induction that the Sierpinski gasket is Pascal's triangle modulo 2. puz(N) seems to look very much like the Sierpinski gasket with nearest dots connected by edges. In terms of Pascal's triangle, puz(N) combines nodes corresponding to odd entries of Pascal's triangle with the nodes 1 unit (whatever this may mean) apart linked by an edge. Since Pascal's triangle consists of binomial coefficients this suggests a question answered more than 100 years ago by Edouard Lucas (1842-1891): what is the parity of
By now, we have established a solid base to be able to answer this question with little additional effort. First, let's present Pascal's triangle in its original, rectangular form. The apex goes to the upper left corner and the entries grow right and downward. The rows and columns are numbered starting with 0. We shall be detecting even entries in a process modeled after the trema removal algorithm.

The key to understanding the diagram is the binary representation of the row and column indices. In the gray square (that looks like a rectangle), all indices (numbers,
Now, this is immediate that
Now I state the Lucas theorem:
Theorem (E. Lucas)
C(n, m) is odd iff Am ⊂ An.
For example, A17 ⊂ A23 and, therefore,
As another example, 2n is the first index to have 1 in the n-th binary position. All its other digits are 0. Therefore,
The proof follows from the algebraic definition of the binomial coefficients:
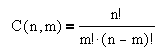
implying k·C(pa, k) = pa·C(pa-1, k-1) which shows that C(pa, k)
is divisible by p wheneverDenoting N = pa, for p prime the binomial theorem modulo p becomes
| (1) | (1 + x)N = 1 + xN (mod p). |
The most general theorem due to Lucas deals with arbitrary n, m, and a prime number p. The theorem deals with representations of n and m in base p:
Theorem (E. Lucas)
Let n = (axax-1...a0)p and m = (byby-1...b0)p. Let
C(n, m) = C(az, bz) · C(az-1, bz-1) ·...· C(a0, b0) (mod p).
Proof
The assertion follows from (1).
C(n, m) is the coefficient by xm in the expansion of (1 + x)n. But
| (1 + x)n | = (1 + x)azpz·(1 + x)az-1pz-1·...·(1 + x)a0p0 | (mod p) |
| = [(1 + x)pz]az·[(1 + x)pz-1]az-1·...·[(1 + x)p0]a0 | (mod p) | |
| = (1 + xpz)az·(1 + xpz-1)az-1·...·(1 + xp0)a0 | (mod p). |
The power xm, with m = (bzbz-1...b0)p, comes up in this expansion only as a product of xbzpz from the first term, xbz-1pz-1 from the second and so on, thus proving Lucas' theorem in its most general form.
Remark
While constructing puz(N) with N growing, we might want to keep the total length of one side of the triangle constant. It can be shown that thus defined sequence of point sets, puz(N), indeed converges to the Sierpinski gasket. Convergence is established in the framework of metric spaces with the Hausdorff distance.
References
- I. Aharoni, From Tower of Hanoi to Pascal's Triangle, Alefefes, #4, 1996 (in Hebrew)
- O. Ore, Graphs and Their Uses, MAA, 1990
- V. H. Moll, Numbers and Functions: From a Classical-Experimental Mathematician's Point of View, AMS, 2012
- I. Stewart, Another Fine Math You've Got Me Into, W.H.Freeman & Co, 1992
- I. Stewart, Game, Set and Math, Penguin Books, 1989
- D. Wells, You Are a Mathematician, John Wiley & Sons, 1995
About Fractals
- Dot Patterns, Pascal Triangle and Lucas Theorem
- Sierpinski Gasket Via Chaos Game
- The Chaos Game: Address Space vs IFS
- Sierpinski Gasket By Common Trema Removal
- Sierpinski Gasket By Trema Removal
- Sierpinski's Gasket and Dihedral Symmetry
- Collage Theorem And Iterated Function Systems
- Variations on the Theme of (Triangular) Tremas
- Variations on the Theme of (Rectangular) Tremas
- Sierpinski Gasket and Tower of Hanoi
- Fractal Curves and Dimension
- Color Cycling on the Mandelbrot Set
- Iterations and the Mandelbrot Set
- Mandelbrot and Julia sets
- Emergence of Chaos
- Logistic Model
- Weird curves bound normal areas
- Exercise with Square Spiral
Pascal's Triangle and the Binomial Coefficients
- Binomial Theorem
- Arithmetic in Disguise
- Construction of Pascal's Triangle
- Dot Patterns, Pascal Triangle and Lucas Theorem
- Integer Iterations on a Circle
- Leibniz and Pascal Triangles
- Lucas' Theorem
- Lucas' Theorem II
- Patterns in Pascal's Triangle
- Random Walks
- Sierpinski Gasket and Tower of Hanoi
- Treatise on Arithmetical Triangle
- Ways To Count
- Another Binomial Identity with Proofs
- Vandermonde's Convolution Formula
- Counting Fat Sets
- e in the Pascal Triangle
- Catalan Numbers in Pascal's Triangle
- Sums of Binomial Reciprocals in Pascal's Triangle
- Squares in Pascal's Triangle
- Cubes in Pascal's Triangle
- Pi in Pascal's Triangle
- Pi in Pascal's Triangle via Triangular Numbers
- Ascending Bases and Exponents in Pascal's Triangle
- Determinants in Pascal's Triangle
- Tony Foster's Integer Powers in Pascal's Triangle
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73512456
