Counting Fat Sets

We start with the set \(\mathbb{N}_{n}=\{1,2,\ldots,n\}\). A subset \(A\subset \mathbb{N}_{n}\) is said to be fat if, for every \(x\in A\), \(x\ge |A|\), where \(|A|\) is the cardinality of, i.e., the number of elements in, \(A\). (Fat sets have been introduced by George Andrews.)

As an example, with \(n=4\), the sets \(\emptyset\), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{4\}\), \(\{2,3\}\), \(\{2,4\}\), \(\{3,4\}\) are fat subsets of \(\mathbb{N}_{n}\), while the sets \(\{1,2\}\), \(\{1,3\}\), \(\{1,4\}\), \(\{1,2,3\}\), \(\{1,2,4\}\), \(\{1,3,4\}\), \(\{2,3,4\}\), and \(\{1,2,3,4\}\) are not.

How many fat subsets are there in \(\mathbb{N}_{n}\)? Let's denote that number \(f_n\). We shall prove a recursive formula:

The number \(f_n\) of fat subsets of \(\mathbb{N}_{n}\) satisfies the recurrence

\(f_{n+1}\) = \(f_n\) + \(f_{n-1}\), \(n\ge 2\),

with \(f_{1}=2\) and \(f_{2}=3\).

Proof

Let \(A\subset\mathbb{N}_{n}\) is fat. There are two possibilities: \(n\in A\) and \(n\notin A\). In the latter case, \(A\) is a fat subset of \(\mathbb{N}_{n-1}\) and counts in \(f_{n-1}\). Assume, \(n\in A\). In that case, \(1\notin A\), because, otherwise, we would have \(|A|\ge 2\gt 1\), making \(A\) non-fat. Define \(B=A\setminus\{n\}\), and \(C=\{x-1:\space x\in B\}\). \(C\) is then a fat subset of \(\mathbb{N}_{n-2}\). We see that any fat subset \(A\) of \(\mathbb{N}_{n}\) is either a fat subset of \(\mathbb{N}_{n-1}\) or uniquely corresponds to a fat subset of \(\mathbb{N}_{n-2}\). The converse is also true, thus proving the recurrence. In addition, \(A\subset\mathbb{N}_{1}\) has only two fat subset, \(\emptyset\) and \(\{1\}\), while \(A\subset\mathbb{N}_{2}\) has three, \(\emptyset\), \(\{1\}\), and \(\{2\}\).

Obviously, \(\{f_n\}\) is a "shifted" Fibonacci sequence \(\{F_n\}\), where \(F_0=F_1=1\): \(f_n=F_{n+2}\).

There is another way to count the fat subsets of \(A\subset\mathbb{N}_{n}\).

There is only one way to pick the empty set. There are \({n \choose 1}\) ways to select a one-element subset. Since \(1\) couldn't be included in fat subsets of more than \(1\) element, there are \({n-1 \choose 2}\) \(2\)-element fat subsets. For a similar reason, \(2\) is excluded from fat subsets with more than \(2\) elements so that there are \({n-2 \choose 3}\) \(3\)-element subsets, and so on. The question is where do we stop? This depends on the parity of \(n\):

\( f_{n}= \begin{cases} {n+1 \choose 0}+{n \choose 1}+{n-1 \choose 2}+\ldots+{(n+1)/2 \choose (n+1)/2},& \text{if}\space n\space \text{is odd} \\ {n+1 \choose 0}+{n \choose 1}+{n-1 \choose 2}+\ldots+{(n+2)/2 \choose n/2},& \text{if}\space n\space \text{is even} \end{cases} \)

Remarkably, sums like these appear in the diagonals of the Pascal triangle:

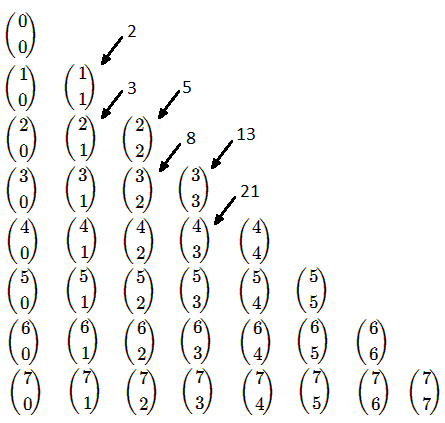
summing up diagonals in the Pascal triangle

Using the shorthand, \(\displaystyle f_{n}=\sum_{k=0}^{N}{n+1-k \choose k}\), where \(N=(n+1)/2\) if \(n\) is odd and \(N=n/2\) if \(n\) is even.

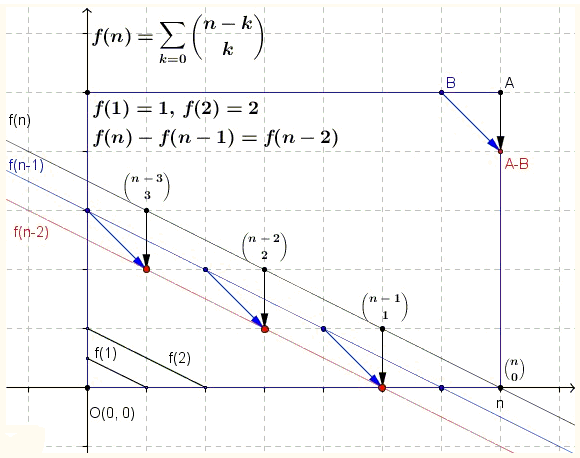
It could be shown that such sums satisfy the Fibonacci recurrence. Vladimir Nikolin came up with a proof without words of the latter fact:

summing up diagonals in the Pascal triangle & recurrence

References

V. K. Balakrishnan, Theory and Problems of Combinatorics, Schaum's Outline Series, McGraw-Hill, 1995
A. T. Benjamin, J. J. Quinn, Proofs That Really Count: The Art of Combinatorial Proof, MAA, 2003
R. Grimaldi, Fibonacci and Catalan Numbers: an Introduction, Wiley, 2012

Pascal's Triangle and the Binomial Coefficients

Combinatorial Proofs

70539357