Sums of Binomial Reciprocals in Pascal's Triangle

A post at the CutTheKnotMath facebook page by Daniel Hardisky brought to my attention the following pattern in Pascal's triangle:

The sums of the reciprocals of the binomial coefficients over successive diagonals

$\displaystyle\sum_{k=0}^{\infty}\frac{1}{C_{k}^{n+k}}=\frac{n}{n-1},\space n\gt 1.$

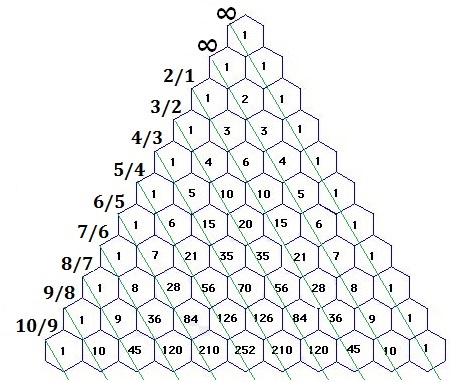
sums of reciprocals in Pascal Triangle

The sum for $n=0$ is obviously $\infty$ and so is for $n=1$ which is just the harmonic series which is known to diverge to infinity.

It appears that such sums, where the binomial reciprocals appear in the denominator, are still very much a research topic. The problem at hand has several known solutions. I chose the one that appeals to the telescoping property of the series involved.

By definition, $\displaystyle\frac{1}{C^{n+k}_{k}} = \frac{n!k!}{(n+k)!} = \frac{n!}{(k+1) (k+2) \cdots (k+n)}.$

Invoking the concept of partial fractions,

$\displaystyle\frac{1}{(k+1)(k+n)}=\frac{1}{n-1}\bigg(\frac{1}{k+1}-\frac{1}{k+n}\bigg),$

which allows us to write

$\displaystyle\frac{n!}{(k+1) (k+2) \cdots (k+n)}=\frac{n!}{n-1}\bigg(\frac{1}{(k+1) \cdots (k+n-1)}- \frac{1}{(k+2) \cdots (k+n)}\bigg).$

It follows that

$\begin{align}\displaystyle\sum_{k=0}^{\infty}\frac{1}{C_{k}^{n+k}} &=\ \frac{n!}{n-1}\sum_{k=0}^{\infty}\bigg(\frac{1}{(k+1) \cdots (k+n-1)}- \frac{1}{(k+2) \cdots (k+n)}\bigg)\\ &=\frac{n!}{n-1}\bigg(\sum_{k=0}^{\infty}\frac{1}{(k+1) \cdots (k+n-1)}-\sum_{k=0}^{\infty}\frac{1}{(k+2) \cdots (k+n)}\bigg)\\ &=\frac{n!}{n-1}\bigg(\sum_{k=0}^{\infty}\frac{1}{(k+1) \cdots (k+n-1)}-\sum_{k=1}^{\infty}\frac{1}{(k+1) \cdots (k+n-1)}\bigg)\\ &=\frac{n!}{n-1}\frac{1}{(k+1) \cdots (k+n-1)}\bigg|_{k=0} =\frac{n!}{n-1}\frac{1}{(n-1)!}=\frac{n}{n-1}. \end{align}$

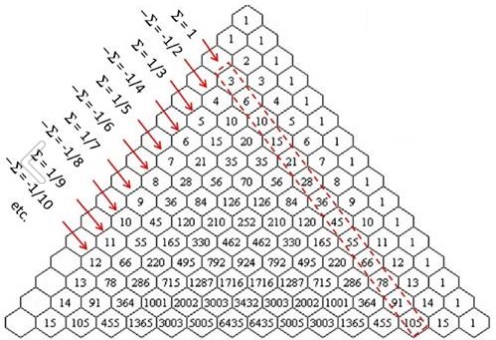
Daniel also observed that there is just one step from $\displaystyle\frac{n}{n-1}$ to the plain reciprocal $\displaystyle\frac{1}{n-1}:$

$\displaystyle\sum_{k=1}^{\infty}\frac{1}{C_{k}^{n+k}}=\frac{1}{n-1},\space n\gt 1.$

Now, the integer reciprocals are known to combine into $\ln 2$ via the Taylor series $\displaystyle\ln (1+x) = \sum_{n=2}(-1)^{n}\frac{x^{n-1}}{n-1}:$

$\displaystyle\ln 2=1-\frac{1}{2}+\frac{1}{3}-\ldots+(-1)^{n}\frac{1}{n-1}+\ldots,$

which leads to the following combination:

$\displaystyle\ln 2=\sum_{n=2}^{\infty}(-1)^{n}\sum_{k=1}^{\infty}\frac{1}{C_{k}^{n+k}}.$

ln(2) in Pascal Triangle

Pascal's Triangle and the Binomial Coefficients

72200750