Vandermonde's Convolution Formula
Vandermonde's Convolution Formula is usually presented as
\(\displaystyle {n+m \choose k} = \sum_{j=0}^{k}{n \choose j}{m \choose k-j}\)
It may also be written in a more symmetric way [Concrete Mathematics, p.169]:
\(\displaystyle {n+m \choose r+s} = \sum_{j}{n \choose r+j}{m \choose s-j} \)
which is obtained from the first one by the substitution \(k=r+s\) and \(j\) replaced with \(r+j\). The latter - because of its symmetry - seems to be easier to memorize. The former seems to arise more naturally in several circumstances and, thus, is easier to prove.
In the symmetrized formula the limits for the index \(k\) of summation are not mentioned explicitly; the sum is, nonetheless finite and the limits of summation are implied by the conditions \({u \choose v}=0\) if \(u\lt v\) or \(v\lt 0\), such that in that formula \(-r\le j\le s\), a visual symmetry spoiler.
Proof 1
This is a combinatorial argument. How many \(k\)-member study teams can be formed out of the group of \(n\) boys and \(m\) girls? By definition, this is the binomial coefficient \({n+m\choose k}\). On the other hand, if a team to consist of \(j\) boys and \(k-j\) girls, then there are \({n \choose j}{m \choose k-j}\) possibilities. The Vandermonde's formula follows by letting \(j\) vary.
Proof 2
This proof was suggested by Vladimir Nikolin and served as an impetus for writing this page. The proof is based on counting the number of paths on a square grid and the following diagram
There are \({x+y \choose x}={x+y \choose y}\) right/up paths from the origin to point \((x,y)\). We count the number of passes from the origin to point \(A(r,n+m-r)\)
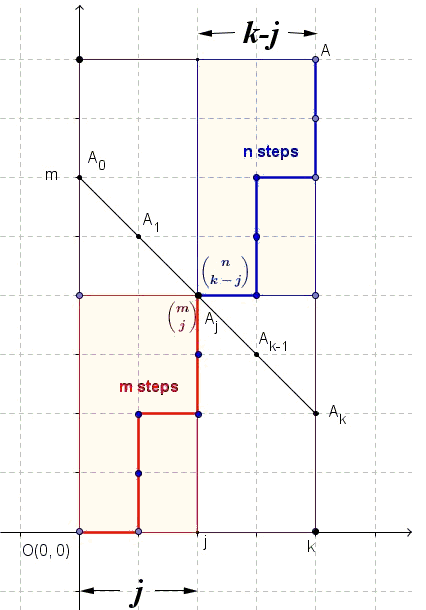
On the one hand, this the number is equal to \({n+m \choose r}\). Now let's have a second look.
Each right/up path from the origin to \(A(r,n+m-r)\) will cross the line \(x+y=m\) in a unique point \(A_{1}(j,m-j)\). There are \({m \choose j}\) paths from the origin to \(A_{1}\). There are \({(n+m-r)-(m-j)+(r-j)\choose r-j}={n \choose r-j}\) paths from \(A_{1}\) to \(A\). Letting \(j\) vary leads to Vandermonde's formula.
Proof 3
The coefficients in the Pascal triangle are exactly the binomial coefficients: the term in position \(x\) in row \(y\) equals \({y\choose x}\); this is defined by the number of SE and SW paths from the top to that location, say, \(B(x,y)\).
Any such path to point \(B(k,n+m)\), crosses (and only once) the row \(n\).
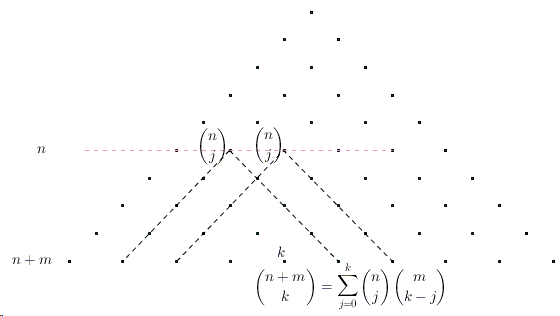
Assume this happens at point \(B(j, n)\) and note that there are \({n \choose j}\) ways to reach that point. Within the Pascal rectangle with the top at \(B(j, n)\), point \(B(k,n+m)\) has different coordinates: \(B(k-j,m)\). Since the paths above and below the \(n\)th row are independent, Vandermonde's formula follows.
Proof 4
Here we just use the binomial theorem:
\(\displaystyle \begin{align} \sum_{k=0}^{n+m}{n+m \choose k}x^{k}&=(x+1)^{n+m}\\ &=(x+1)^{n}(x+1)^{m} \\ &=\sum_{r=0}^{n}{n \choose r}x^{r}\cdot\sum_{s=0}^{m}{m\choose s}x^{s}\\ &=\sum_{k}\bigg[\sum_{r}{n\choose r}{m\choose k-r}\bigg]x^{k}. \end{align} \)
Corollary
\(\displaystyle {2n\choose n}=\sum_{r=0}^{n} {n \choose r}^{2} \)
Proof
By Vandermonde's formula for \(n=m=k\),
\(\displaystyle \begin{align} {2n\choose n} &= {n + n\choose n} \\ &=\sum_{r}{n \choose r}{n \choose n-r}\\ &=\sum_{r}{n \choose r}{n \choose r}, \end{align} \)
because \({n\choose n-r}={n\choose r}\).
References
- A. T. Benjamin, J. J. Quinn, Proofs That Really Count: The Art of Combinatorial Proof, MAA, 2003
- R. Graham, D. Knuth, O. Patashnik, Concrete Mathematics, 2nd edition, Addison-Wesley, 1994.
- V. H. Moll, Numbers and Functions: From a Classical-Experimental Mathematician's Point of View, AMS, 2012
Absolute Value
- Absolute Value
- Importance of the Absolute Value
- Cartesian Coordinate System
- Algebraic Structure of Complex Numbers
- Structure of Hyperreal Numbers
- Farmer and Wife To Catch Rooster and Hen
- Topological Preliminaries
- Proizvolov's Identity
- Absolute Value and 1998 integers
- Optimal Residence
- Sum of Absolute Values
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73597127
