Treatise on Arithmetical Triangle

Blaise Pascal's Treatise on Arithmetical Triangle was written in 1653 and appeared posthumously in 1665. The full text of the Treatise is available in [D. E. Smith's A Source Book in Mathematics, 67-79] and, among other Pascal's works, in volume 33 of the Great Books of the Western World series. The famous arrangement of numbers was known before Pascal's time in China, India and Persia, albeit to a very limited extent. It made its first appearance in Europe in 1527 as the frontispiece of Petrus Apianus (1495-1552) book on arithmetic. It has subsequently appeared [Smith, 510] in Stifel's Arithmetica Integra (1544), Scheubel's (1545), Peletier's (1549), Tartaglia's (1556), Bombelli's (1572) and Oughtred's (1631) books. Pascal had to have been familiar with at least some of these publications. Unlike Tartaglia, he never laid claim to the invention of the triangle, although he chose a rather uncommon configuration to study the triangle. In the Treatise he assembled and proved nineteen corollaries (of the definition) and several lemmas and propositions that laid foundation (together with Pascal's correspondence with Fermat) of Probability theory. In particular, he established a formula (which he treated as a problem following the Last Corollary) that in modern notations appears as
| C(n, k) | = | k(k - 1)(k - 2)·...·1 |
Pascal did not have yet the powerful tools, like the coordinate system and mathematical induction so that his notations and proofs were limited to a small portion of the triangle, although the latter could be easily upgraded to confirm to the modern requirements of rigor.
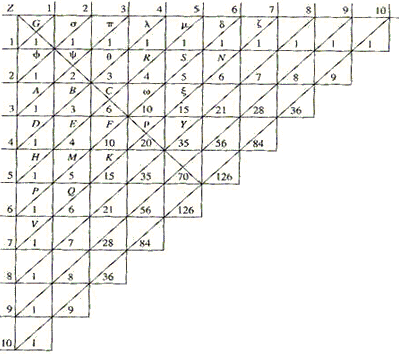
In Pascal's terminology, the rows of the array were called parallel ranks and the columns perpendicular ranks; the numbers occupied the cells; the cells formed triangles with the upper left corner as an apex and the sw-ne diagonals as the bases. The 1 in the upper left corner was called a generator which was repeated along the edges. Pascal allowed for various generators, not just 1. Here is a sample of his style.
Corollary 3
In every arithmetic triangle, each cell is equal to the sum of all those of the preceding perpendicular rank, comprising the cells from its parallel rank to the first, inclusively.
Consider any cell C: I assert that it is equal to B + ψ + σ, which are the cells of the preceding perpendicular rank, from the parallel rank of the cell C to the first parallel rank.
C equals B + θ, θ equals ψ + π, π equals σ. Hence C equals B + ψ + σ.
Corollary 4
In every arithmetic triangle, each cell diminished by unity is equal to the sum of all those which are included between its perpendicular rank and its parallel rank, exclusively.
Consider any cell ξ: I assert that ξ - G equals R + θ + ψ + φ + λ + π + σ + G, which are all the numbers included between the ranks ξωCBA and the rank ξSμ, exclusively.
For ξ equals λ + R + ω, ω equals π + θ + C, C equals σ + ψ + B, B equals G + φ + A, A equals G. Hence ξ equals λ + R + π + θ + σ + ψ + G + φ + G.
Pascal makes a note. I have said in the statement: each cell diminished by unity, because unity is the generator; but if it were another number, it would be necessary to say: each cell diminished by generating number.
Corollary 12
In every arithmetical triangle, of two contiguous cells in the same base the upper is to the lower as the number of cells from the upper to the top of the base is to the number of cells from the lower to the bottom of the base, inclusive.
This one I shall just reformulate in modern notations:
The last of the nineteen corollaries is followed by a remark: Thence many other proportions may be drawn that I have passed over, because they may be easily deduced, and those who would like to apply themselves to it will perhaps find some, more elegant than these which I could present.
References
- H. Eves, Great Moments in Mathematics After 1650, MAA, 1983
- Great Books of the Western World, v 33, Encyclopaedia Britannica, Inc., 1952.
- J. A. Paulos, Beyond Numeracy, Vintage Books, 1992
- D. E. Smith, History of Mathematics, Dover, 1968
- D. E. Smith, A Source Book in Mathematics, Dover, 1959
Pascal's Triangle and the Binomial Coefficients
- Binomial Theorem
- Arithmetic in Disguise
- Construction of Pascal's Triangle
- Dot Patterns, Pascal Triangle and Lucas Theorem
- Integer Iterations on a Circle
- Leibniz and Pascal Triangles
- Lucas' Theorem
- Lucas' Theorem II
- Patterns in Pascal's Triangle
- Random Walks
- Sierpinski Gasket and Tower of Hanoi
- Treatise on Arithmetical Triangle
- Ways To Count
- Another Binomial Identity with Proofs
- Vandermonde's Convolution Formula
- Counting Fat Sets
- e in the Pascal Triangle
- Catalan Numbers in Pascal's Triangle
- Sums of Binomial Reciprocals in Pascal's Triangle
- Squares in Pascal's Triangle
- Cubes in Pascal's Triangle
- Pi in Pascal's Triangle
- Pi in Pascal's Triangle via Triangular Numbers
- Ascending Bases and Exponents in Pascal's Triangle
- Determinants in Pascal's Triangle
- Tony Foster's Integer Powers in Pascal's Triangle
|Activities| |Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73524234
