Squares in Pascal's Triangle
A post at the CutTheKnotMath facebook page by Tony Foster brought to my attention several sightings of square numbers in Pascal's triangle as an expanding pattern:
$\displaystyle C_{2}^{n}+C_{2}^{n+1}=n^2,$
$\displaystyle C_{3}^{n+2}-C_{3}^{n}=n^2,$
$\displaystyle C_{4}^{n+3}-C_{4}^{n+2}-C_{4}^{n+1}+C_{4}^{n}=n^2,$
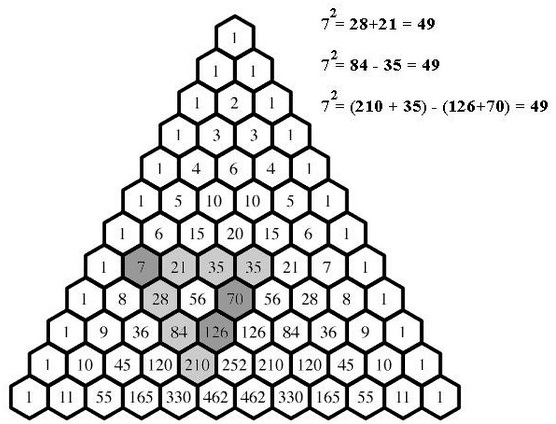
Let's verify what we can, skipping the first one.
$\displaystyle C_{3}^{n+2}-C_{3}^{n}=n^2$
Indeed,
$\begin{align}\displaystyle C_{3}^{n+2}-C_{3}^{n} &= \frac{(n+2)(n+1)n-n(n-1)(n-2)}{3!}\\ &=\frac{n[(n^{2}+3n+2) - (n^{2}-3n+2)]}{3!}\\ &=\frac{n(6n)}{3!}=n^2. \end{align}$
$\displaystyle C_{4}^{n+3}-C_{4}^{n+2}-C_{4}^{n+1}+C_{4}^{n}=n^2$
Indeed, say,
$\begin{align} A &=(n+3)(n+2)(n+1)n-(n+2)(n+1)n(n-1)\\ &=(n+2)(n+1)n[(n+3)-(n-1)]\\ &=4(n+2)(n+1)n. \end{align}$
And, also,
$\begin{align} B&=(n+1)n(n-1)(n-2)+n(n-1)(n-2)(n-3)\\ &=n(n-1)(n-2)n[(n+1)-(n-3)]\\ &=4n(n-1)(n-2). \end{align}$
So that, as before,
$\begin{align} A-B &= 4n[((n+2)(n+1))-((n-1)(n-2))]\\ &=4n\cdot (6n)=24n^2. \end{align}$
It follows that
$\displaystyle C_{4}^{n+3}-C_{4}^{n+2}-C_{4}^{n+1}+C_{4}^{n}=\frac{24n^2}{4!}=n^2.$
Are there any more? What would be the next identity? Probably this
$\displaystyle C_{5}^{n+4}-C_{5}^{n+3}-C_{5}^{n+2}-C_{5}^{n+1}+C_{5}^{n}=n^2.$
Let's check:
$\begin{align} \mbox{For}\space n=7:&\space \space 462-252-126-56+21=49=7^2,\\ \mbox{For}\space n=8:&\space \space 792-462-252-126+56=8\ne 8^2. \end{align}$
So, this is where we stop - at least for now.
However, Tony discovered an additional pattern and came up with a proof of its validty:
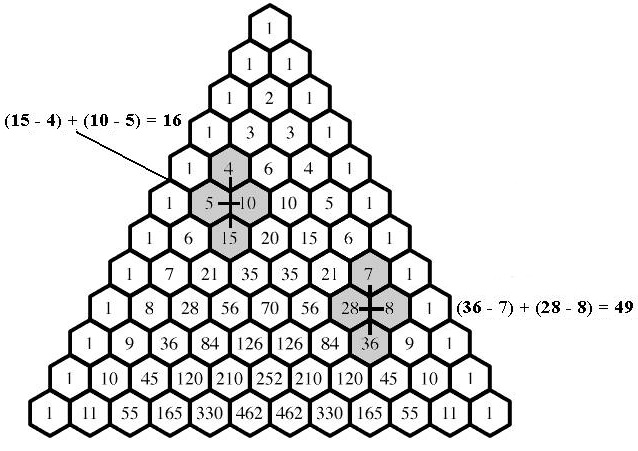
$\displaystyle C^{n+2}_{1}-C^{n}_{1}+C^{n+1}_{2}-C^{n+1}_{1}=n^2.$
$\displaystyle\begin{align} C^{n+2}_{1}-C^{n}_{1}+C^{n+1}_{2}-C^{n+1}_{1}&=\frac{(n+2)(n+1)}{2}-n+\frac{(n+1)n}{2}-(n+1)\\ &=\frac{(n^{2}+3n+2-2n)+(n^2+n-2n-2)}{2}\\ &=\frac{2n^2}{2}=n^2. \end{align}$
Pascal's Triangle and the Binomial Coefficients
- Binomial Theorem
- Arithmetic in Disguise
- Construction of Pascal's Triangle
- Dot Patterns, Pascal Triangle and Lucas Theorem
- Integer Iterations on a Circle
- Leibniz and Pascal Triangles
- Lucas' Theorem
- Lucas' Theorem II
- Patterns in Pascal's Triangle
- Random Walks
- Sierpinski Gasket and Tower of Hanoi
- Treatise on Arithmetical Triangle
- Ways To Count
- Another Binomial Identity with Proofs
- Vandermonde's Convolution Formula
- Counting Fat Sets
- e in the Pascal Triangle
- Catalan Numbers in Pascal's Triangle
- Sums of Binomial Reciprocals in Pascal's Triangle
- Squares in Pascal's Triangle
- Cubes in Pascal's Triangle
- Pi in Pascal's Triangle
- Pi in Pascal's Triangle via Triangular Numbers
- Ascending Bases and Exponents in Pascal's Triangle
- Determinants in Pascal's Triangle
- Tony Foster's Integer Powers in Pascal's Triangle
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73602476
