Dot Patterns, Pascal Triangle and Lucas Theorem
In the drawing area of the applet below, we have either rows of digits or circles with colors corresponding to the digits. Patterns in the drawing area are defined row-by-row starting from the upper row which consists of clickable digits (or circles.) The value p of a node is defined by values (q1 and q2) of the two nodes immediately above it according to the following formula:
where N is the modulus of the arithmetic used. Think of the applet as presenting a finite view of an infinite lattice of nodes filling the lower half plane. All omitted nodes are assigned the value of 0. The applet has the following controls:
- Every dot in the upper row is clickable. With every click the digit (or the corresponding color) cycles through the sequence of residues 0, 1, 2, 3, ..., N-1.
- When creating a new pattern, you can select to get a single nonzero digit in the upper row, or a random pattern, or the whole upper row carrying the same digit (1).
- By checking "Multiplies" you request to associate all nonzero digits with a single color. In this case, the pattern consists of two colors only with 0 using the foreground color. So that the colors are in a sense reversed.
- You can also chose to see a pure triangle with a single node in the upper row. The apex of the triangle is still clickable.
(Please note that when the number of rows is close to the maximum of 50, the drawing is slow. Be patient.)
As of 2018, Java plugins are not supported by any browsers (find out more). This Wolfram Demonstration, Pascal-like Triangles Mod k, shows an item of the same or similar topic, but is different from the original Java applet, named 'Patterns'. The originally given instructions may no longer correspond precisely.
(image below from deprecated 'Patterns' applet)
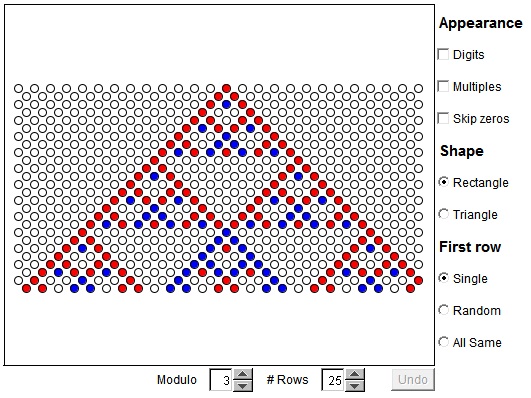
You are to investigate the distribution of 0s in rows of the pattern emanating from a single dot.
About Fractals
- Dot Patterns, Pascal Triangle and Lucas Theorem
- Sierpinski Gasket Via Chaos Game
- The Chaos Game: Address Space vs IFS
- Sierpinski Gasket By Common Trema Removal
- Sierpinski Gasket By Trema Removal
- Sierpinski's Gasket and Dihedral Symmetry
- Collage Theorem And Iterated Function Systems
- Variations on the Theme of (Triangular) Tremas
- Variations on the Theme of (Rectangular) Tremas
- Sierpinski Gasket and Tower of Hanoi
- Fractal Curves and Dimension
- Color Cycling on the Mandelbrot Set
- Iterations and the Mandelbrot Set
- Mandelbrot and Julia sets
- Emergence of Chaos
- Logistic Model
- Weird curves bound normal areas
- Exercise with Square Spiral
Pascal's Triangle and the Binomial Coefficients
- Binomial Theorem
- Arithmetic in Disguise
- Construction of Pascal's Triangle
- Dot Patterns, Pascal Triangle and Lucas Theorem
- Integer Iterations on a Circle
- Leibniz and Pascal Triangles
- Lucas' Theorem
- Lucas' Theorem II
- Patterns in Pascal's Triangle
- Random Walks
- Sierpinski Gasket and Tower of Hanoi
- Treatise on Arithmetical Triangle
- Ways To Count
- Another Binomial Identity with Proofs
- Vandermonde's Convolution Formula
- Counting Fat Sets
- e in the Pascal Triangle
- Catalan Numbers in Pascal's Triangle
- Sums of Binomial Reciprocals in Pascal's Triangle
- Squares in Pascal's Triangle
- Cubes in Pascal's Triangle
- Pi in Pascal's Triangle
- Pi in Pascal's Triangle via Triangular Numbers
- Ascending Bases and Exponents in Pascal's Triangle
- Determinants in Pascal's Triangle
- Tony Foster's Integer Powers in Pascal's Triangle
73595645 |
Copyright © 1996-2018 Alexander Bogomolny |
