Tony Foster's Integer Powers in Pascal's Triangle
Source
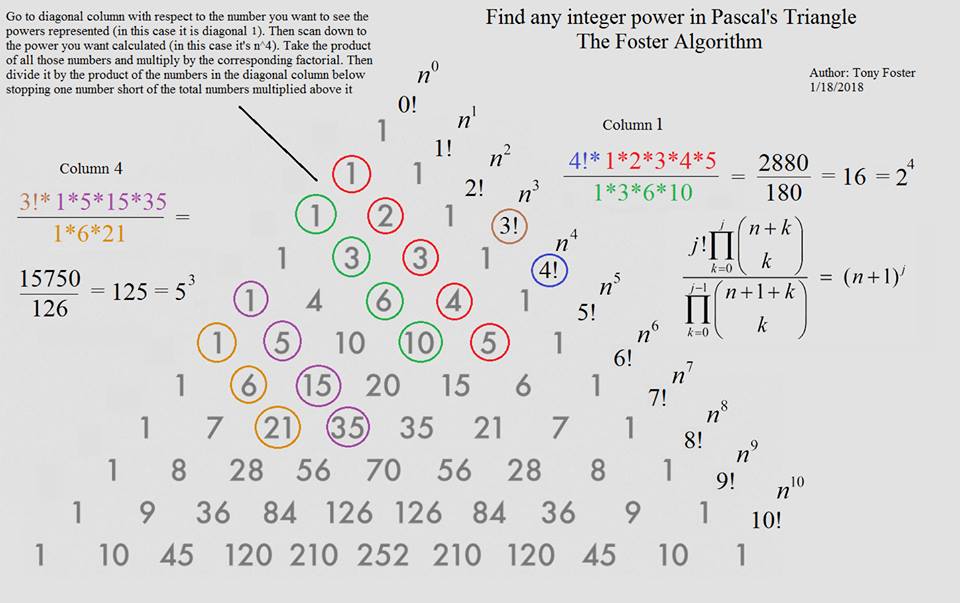
Problem
For integer $n,j\gt 1,$ we have
$\displaystyle \frac{\displaystyle j!\prod_{k=0}^{j}{n+k\choose k}}{\displaystyle \prod_{k=0}^{j-1}{n+1+k\choose k}}=(n+1)^j.$
Note that the multiplicands in the two products come from successive rows (or columns) of Pascals's triangle.
Solution 1
We start with an obvious $\displaystyle {n+1+k\choose k}=\frac{n+1+k}{n+1}{n+k\choose k}.$ Using that,
$\displaystyle \begin{align} \frac{\displaystyle j!\prod_{k=0}^{j}{n+k\choose k}}{\displaystyle \prod_{k=0}^{j-1}{n+1+k\choose k}}&=\frac{\displaystyle j!\prod_{k=0}^{j-1}{n+k\choose k}\cdot {n+j\choose j}}{\displaystyle \prod_{k=0}^{j-1}\frac{n+1+k}{n+1}\cdot\prod_{k=0}^{j-1}{n+k\choose k}}\\ &=\frac{\displaystyle j!{n+j\choose j}}{\displaystyle \prod_{k=0}^{j-1}\frac{n+1+k}{n+1}}=\frac{(n+j)!}{n!}\cdot\frac{\displaystyle (n+1)^j}{\displaystyle\prod_{k=0}^{j-1}(n+1+k)}\\ &=\frac{(n+1)^j\cdot (n+j)!}{(n+j)!}=(n+1)^j. \end{align}$
Solution 2
We'll use induction on $j.$ Let $\displaystyle F(j)=\frac{\displaystyle j!\prod_{k=0}^{j}{n+k\choose k}}{\displaystyle \prod_{k=0}^{j-1}{n+1+k\choose k}}$ and assume $F(m)=(n+1)^m,$ for some $m\gt 0.$ Then
$\displaystyle \begin{align} \frac{F(m+1)}{F(m)}&=\frac{\displaystyle (m+1){n+m+1\choose m+1}}{\displaystyle {n+1+m\choose m}}\\ &= \frac{(m+1)(n+m+1)!}{n!(m+1)!}\cdot\frac{(n+1)!m!}{(n+1+m)!}=n+1, \end{align}$
implying $F(m+1)=F(m)(n+1)=(n+1)^m(n+1)=(n+1)^{m+1}.$
Acknowledgment
This is Tony Foster's invention that he kindly shared on the CutTheKnotMath facebook page. Solution 1 is a slight modification of his original proof.
The above is a generalization of Tony's previous discovery.
Pascal's Triangle and the Binomial Coefficients
- Binomial Theorem
- Arithmetic in Disguise
- Construction of Pascal's Triangle
- Dot Patterns, Pascal Triangle and Lucas Theorem
- Integer Iterations on a Circle
- Leibniz and Pascal Triangles
- Lucas' Theorem
- Lucas' Theorem II
- Patterns in Pascal's Triangle
- Random Walks
- Sierpinski Gasket and Tower of Hanoi
- Treatise on Arithmetical Triangle
- Ways To Count
- Another Binomial Identity with Proofs
- Vandermonde's Convolution Formula
- Counting Fat Sets
- e in the Pascal Triangle
- Catalan Numbers in Pascal's Triangle
- Sums of Binomial Reciprocals in Pascal's Triangle
- Squares in Pascal's Triangle
- Cubes in Pascal's Triangle
- Pi in Pascal's Triangle
- Pi in Pascal's Triangle via Triangular Numbers
- Ascending Bases and Exponents in Pascal's Triangle
- Determinants in Pascal's Triangle
- Tony Foster's Integer Powers in Pascal's Triangle
|Contact| |Front page| |Contents| |algebra|
Copyright © 1996-2018 Alexander Bogomolny73579658
