Invariant Area Sweep Implies Pythagorean Theorem
Think of a right triangle that rotates around one of its acute vertices.
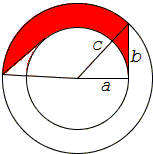
The right-angled vertex then traces a circle of radius \(a\), whilst the second acute vertex traces a circle of radius \(c\). The leg \(b\) of the triangle is tangent to the small circle and sweeps the area between the two circles. The Pythagorean theorem assures that the area of the ring (annulus) is \(\pi b^{2}\).
The applet below illustrates a thought experiment. In two concentric circles of radii \(a\) and \(c\), \((a \lt c),\) the semitangent to the small circle contained by the big circle is allowed to rotate. The semitangent of length \(b\), sweeps an area which after a complete turn covers the ring between the two circles. The area of the ring is \(\pi(c^{2} - a^{2})\). Were it possible to find a proof independent of the Pythagorean theorem that the area swept by the \(b\) segment is indeed \(\pi b^{2}\), we would get an additional proof of the Pythagorean theorem itself.
| What if applet does not run? |
The first three figures below serve to demonstrate that the portion of the ring swept by leg \(b\) due to a turn by a certain angle equals the area of the ring sector formed by that angle.
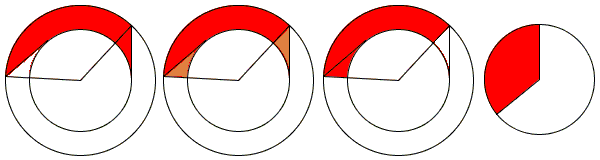
The fourth figure is to remind that the latter area, in turn, equals the area of the circular sector of radius \(b\) formed by the same angle.
[Mark Levi, p. 17] offers this explanation:
Here is a heuristic argument. The ring is swept by a moving segment of length \(b\) as the segment executes two simultaneous motions: sliding (in the direction of the segment) and rotating around the trailing end point of the segment. The key observation is this: the sliding motion does not affect the rate at which the segment sweeps the area. In other words, by subtracting the sliding velocity, and thus making the segment rotate in place around the trailing point, we do not affect the rate at which the segment sweeps the are.
This is not a proof of the claimed equality of the areas but an argument of the sort which frequently used in mathematical research and discourse. As Archimedes explained (at the beginning of his Method [Stein, p. 33, Archimedes, p. 570]) to his friend Eratosthenes:
It is easier to supply the proof when we have previously acquired, by the method, some knowledge of the questions than it is to find it without any previous knowledge.
Employing Calculus, we may observe that leg \(b\) participates locally in two motions: one sliding in its own direction and second rotating around one of its ends. The first does not contribute to sweeing the area. The second contributes exactly as much as it would if one of its ends were fixed, which would give exactly \(\frac{1}{2}b^{2}\theta\) for the area covered due to a turn through angle \(\theta\), making the area of the wholering (i.e., when \(\theta = 2\pi\)) \(\pi b^{2}\). (We use the same argument elsewhere.)
(T. M. Apostol and M. Mamikon published several papers devoted to the invariance of areas under the sweep of a segment.)
For a particular case of annulus there is a simpler proof of even a more general fact.
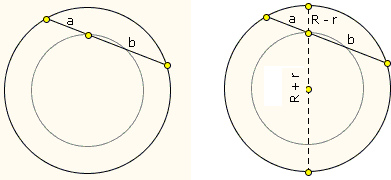
Let there be a chord in a circle \(C(O)\) of radius \(R\) that is divided by an interior point \(P\) into two pieces of length \(a\) and \(b\). When the chords glides over \(C(O)\), \(P\) describes another circle. This is a particular case of Holditch's theorem that the area of the annulus between the two circles is \(\pi ab\), independent of \(R\). We shall prove this fact directly.
Draw a diameter of \(C(O)\) through \(P\). \(P\) divides this diameter into two pieces \(R + r\) and \(R - r\), where \(r\) is the radius of the small circle. By the Intersecting Chords theorem, \(ab = (R + r)(R - r) = R^{2} - r^{2}\) so that
\[ \pi ab = \pi (R + r)(R - r) = \pi R^{2} - \pi r^{2}. \]
This is true for any lengths \(a\) and \(b\). In particular, this is true for \(a = b\).
References
- T. M. Apostol and M. Mamikon, Tangents and Subtangents Used to Calculate Areas, American Mathematical Monthly, 109(10), 2002 pp. 900-908.
- Archimedes, The Method Treating of Mechanical Problems, Great Books of the Western World, v 11, The University of Chicago, 1952
- M. Levi, The Mathematical Mechanic, Princeton University Press, 2009
- M. Mamikon, Annular Rings of Equal Area, Math Horizons, 5(3), 1997 pp. 5-8
- S. Stein, Archimedes: What Did He Do Besides Cry Eurika?, MAA, 1999
|Activities| |Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73596814
