A simple integral, III

The problem has been shared on facebook by George Apostolopoulos and solved (Solution 1) by Mehmet Şahin. Amit Itagi has contributed Solution 2, N. N. Talleb Solution 3. Later on, Dan Sitaru submitted an amendment to the problem graceously offered by the problem authors.

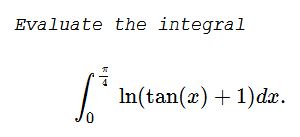
simple integral, almost without calculus

There is a way to find this integral without actually computing integrals at all. Well, almost.

Evaluate the integral

$\displaystyle \int_{0}^{\frac{\pi}{4}}\ln (\tan(x)+1)dx.$

Solution 1

Let's make a substitution, say, $x=\displaystyle \frac{\pi}{4}-t.\,$ Then $dx=-dt\,$ and

$\displaystyle \begin{align} I &= \int_{0}^{\frac{\pi}{4}}\ln (\tan(x)+1)dx\\ &=\int_{\frac{\pi}{4}}^{0}\ln \left(\tan\left(\frac{\pi}{4}-t\right)+1\right)(-dt)\\ &=\int_{0}^{\frac{\pi}{4}}\ln \left(\frac{1-\tan(t)}{1+\tan(t)}+1\right)dt\\ &=\int_{0}^{\frac{\pi}{4}}\ln \left(\frac{2}{1+\tan(t)}\right)dt\\ &=\int_{0}^{\frac{\pi}{4}}\ln 2dt-\int_{0}^{\frac{\pi}{4}}\ln(1+\tan(t))dt\\ &=\frac{\pi}{4}\ln(2)-I, \end{align}$

implying that $\displaystyle 2I=\frac{\pi}{4}\ln(2),\,$ or $\displaystyle I=\frac{\pi}{8}\ln(2).$

Solution 2

$\begin{align} \ln (1+\tan x) &= \ln (\sin x + \cos x) - \ln (\cos x) \\ \nonumber &= \ln\left[\sqrt{2}\cos\left(\frac{\pi}{4}-x\right)\right] - \ln(\cos x) \\ &=\frac{\ln 2}{2} + \ln\left[\cos\left(\frac{\pi}{4}-x\right)\right] - \ln(\cos x) \end{align}$

$\begin{align} \int_0^{\pi/4} \ln(1+\tan x) dx &= \frac{\pi}{8}\ln 2 + \int_0^{\pi/4} \ln\left[\cos\left(\frac{\pi}{4}-x\right)\right] dx - \int_0^{\pi/4} \ln(\cos x) dx \\ &= \frac{\pi}{8}\ln 2 - \int_{\pi/4}^{0} \ln(\cos x) dx - \int_0^{\pi/4} \ln(\cos x) dx \\ &= \frac{\pi}{8}\ln 2 + \int_0^{\pi/4} \ln(\cos x) dx - \int_0^{\pi/4} \ln(\cos x) dx \\ &= \frac{\pi}{8}\ln 2 \end{align}$

Solution 3

By substitution $=\tan(x),\,$

$\displaystyle \int_{0}^{frac{\pi}{4}}\log (\tan(x)+1)dx=\int_{0}^{1}\frac{\log (u+1)}{u^2+1}.$

We substitute again: $\displaystyle v=\frac{1-u}{1+u}:$

$\displaystyle \begin{align} \int_{0}^{1}\frac{\log (u+1)}{^2+1} &=\int_{0}^{1}\frac{\log(2)-\log (v+1)}{v^2+1}dv\\ &=[\arctan(v)\log(2)]^{1}_{0}-\int_0^1\frac{\log(v+1)}{v^2+1}dv\\ &=\frac{1}{4}\pi\log(2)-\int_0^1\log(v+1){c^2+1}dv \end{align}$

It follows that $\displaystyle \int_0^1\log(v+1){c^2+1}dv=\frac{1}{4}\pi\log(2)$.

Amendement

If $a,b\in\displaystyle\left(0,\frac{\pi}{4}\right)\,$ and $a+b=\displaystyle\frac{\pi}{4}\,$ then evaluate the integral

$\displaystyle \int_{a}^{b}\ln (\tan(x)+1)dx.$

Solution

Make a substitution $x=a+b-t=\displaystyle\frac{\pi}{4}.\,$ Then $x'(t)=-1\,$ $x(a)=b,\,$ and $x(b)=a\,$ so that

$\displaystyle\begin{align} I&=\int_{a}^{\frac{\pi}{4}b}\ln (\tan(x)+1)dx\\ &=\int_{a}^{\frac{\pi}{4}b}\ln (\tan\left(\frac{\pi}{4}-t\right)+1)(-1)dx\\ &=\int_{a}^{b}\ln\left(1+\frac{1-\tan t}{1+\tan t}\right)dt\\ &=\int_{a}^{b}\ln\left(\frac{1+\tan t+1-\tan t}{1+\tan t}\right)dt\\ &=\int_{a}^{b}\ln\left(\frac{2}{1+\tan t}\right)dt\\ &=\ln 2\int_{a}^{b}dt-\int_{a}^{b}\ln(1+\tan x)dx. \end{align}$

It follows that $2I=(b-a)\ln 2,\,$ i.e., $\displaystyle I=\frac{b-a}{2}\ln 2.$

72091512