An Integral Inequality from the RMM
Source
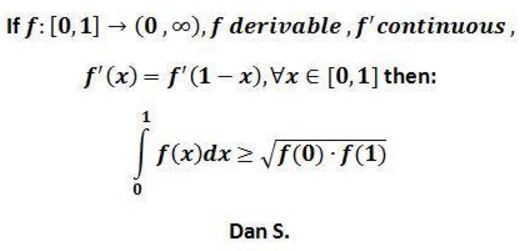
Problem
If $f:\,[0,1]\to (0,\infty)\,$ is continuously differentiiable and satisfies $f'(x)=f'(1-x)\,$ on $[0,1],\,$ then
$\displaystyle \int_0^1f(x)dx\ge\sqrt{f(0)f(1)}.$
Proof 1
The condition $f'(x)=f'(1-x)\;$ implies $f(x)+f(1-x)=C,\;$ a constant, for $x\in [0,1].$ This is a kind of situation that has been considered elsewhere on three different occasions.
If $\displaystyle I=\int_{0}^{1}f(x)dx,\;$ then
$\displaystyle 2I=\int_{0}^{1}(f(x)+f(1-x))dx=C=f(x)+f(1-x),\;$
for any $x\in [0,1].\;$ In particular, with $x=0,\;$ $2I=f(0)+f(1).\;$ It then follows by the AM-GM inequality that
$\displaystyle I=\frac{f(0)+f(1)}{2}\ge\sqrt{f(0)f(1)}.$
Proof 2
With $\displaystyle I=\int_{0}^{1}f(x)dx,\;$ and integrating by parts,
$\displaystyle\begin{align} I&= \left[xf(x)\right]^1_0-\int_0^1xf'(x)dx\\ &=f(1)-\int_0^1xf'(x)dx\\ &=f(1)+\int_0^1xf'(1-x)d(1-x)\\ &=f(1)+\int_0^1f'(1-x)d(1-x)-\int_0^1(1-x)f'(1-x)d(1-x)\\ &=f(1)+\int_1^0f'(x)dx-\int_1^0xf'(x)dx\\ &=f(1)+f(0)+\int_{1}^{0}\left[\frac{d}{dx}(x)\int_{1}^{0}f'(x)dx\right]dx\\ &=f(1)+f(0)-\int_0^1f(x)dx\\ &=f(1)+f(0)-I, \end{align}$
implying
$\displaystyle I=\frac{f(0)+f(1)}{2}\ge\sqrt{f(0)f(1)}.$
Acknowledgment
The problem from the Romanian Mathematical Magazine has been posted at the CutTheKnotMath facebook page by Dan Sitaru, along with the solution (Proof 1) by Safal Das Biswas (India). To avoid repetition I took the liberty of shortening the proof, using links to the older pages at this site. Proof 2 is by Diego Alvariz (India).
- A simple integral, I
- A simple integral, II
- A simple integral, III
- Another simple integral
- Yet Another Simple Integral
- Integral in Normal Distribution
- Sum Without Adding
- An Integral Inequality from the RMM
- Another Integral Inequality from the RMM
- A Triple Integral Inequality
- An Integral from the RMM
- An Integral Identity with Two Functions
- A Simple Integral of a Peculiar Function
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73575415
