An Integral from the RMM
Problem
Solution 1
First note that
$\displaystyle\begin{align} I&=\int_0^1\frac{\sqrt{1-x}+\sqrt{x}}{1+\sqrt{2x}}f(x)dx\\ &=\int_0^1\frac{\sqrt{x}+\sqrt{1-x}}{1+\sqrt{2(1-x)}}f(1-x)dx. \end{align}$
Consider the function
$\displaystyle\begin{align} g(x)&=\frac{\sqrt{1-x}+\sqrt{x}}{1+\sqrt{2x}}f(x)+\frac{\sqrt{x}+\sqrt{1-x}}{1+\sqrt{2(1-x)}}f(1-x)\\ &=\left(\frac{\sqrt{1-x}+\sqrt{x}}{1+\sqrt{2x}}+\frac{\sqrt{x}+\sqrt{1-x}}{1+\sqrt{2(1-x)}}\right)f(x)\\ &=(\sqrt{x}+\sqrt{1-x})\left(\frac{\sqrt{2(1-x)}-\sqrt{2x}}{1-2x}\right)f(x)\\ &=(\sqrt{x}+\sqrt{1-x})\left(\frac{1-\sqrt{2x}}{1-2x}-\frac{1-\sqrt{2(1-x)}}{1-2x}\right)f(x)\\ &=\sqrt{2}\frac{(\sqrt{1-x}+\sqrt{x})(\sqrt{1-x}-\sqrt{x})}{1-2x}f(x)\\ &=\sqrt{2}\frac{(1-x)-x}{1-2x}f(x)\\ &=\sqrt{2}f(x). \end{align}$
due to the condition $f(x)=f(1-x).\,$ If we now note that $\displaystyle \int_0^1g(x)dx=2I\,$ we'll conclude that
$\displaystyle 2I=\sqrt{2}\int_0^1f(x)dx.$
Solution 2
Making the substitutions,
$\displaystyle \begin{align} &y=x-\frac{1}{2}, \\ &g(y)=f(y+1/2), \\ &h(y)=\frac{\sqrt{1-2y}+\sqrt{1+2y}}{1+\sqrt{1+2y}}-1, \end{align}$
we have
$\displaystyle \begin{align} &\int_{0}^{1}\left[\frac{\sqrt{1-x}+\sqrt{x}}{1+\sqrt{2x}}-\frac{1}{\sqrt{2}}\right]f(x)dx \\ &\qquad\qquad =\frac{1}{\sqrt{2}}\int_{-1/2}^{1/2}\left[\frac{\sqrt{1-2y}+\sqrt{1+2y}}{1+\sqrt{1+2y}}-1\right]g(y)dy\\ &\qquad\qquad =\frac{1}{\sqrt{2}}\int_{-1/2}^{1/2} h(y)g(y)dy. \end{align}$
To prove that the integral is $0$, we prove that $g(y)$ is even and $h(y)$ is odd.
$\displaystyle g(y)=f(y+1/2)=f(1-(y+1/2))=f(1/2-y)=g(-y)$.
$h(0)=0$. For $y\neq 0$,
$\displaystyle \begin{align} h(y)&=\frac{\sqrt{1-2y}+\sqrt{1+2y}}{1+\sqrt{1+2y}}-1 \\ &=\frac{\sqrt{1-2y}-1}{\sqrt{1+2y}+1} \\ &=\frac{(\sqrt{1-2y}-1)(\sqrt{1+2y}-1)}{2y}. \end{align}$
Thus, $h(-y)=-h(y)$.
Solution 3
Let $\displaystyle g(x)=\frac{\sqrt{1-x}+\sqrt{x}}{\sqrt{2 x}+1}$. We note that $g(x)+g(1-x)=\sqrt{2}$.
Now let $u=1-x$ and by substitution:
$\displaystyle \int_0^1 g(x) f(x)\, dx =\int_0^1 g (1-u) f (1-u) \, du=\int_0^1 g (1-u) f (u) \, du$
We have
$\displaystyle\begin{align}\int_0^1 f(x) (g(1-x)+g(x)) \, dx&=2 \int_0^1 f(x) g(x) \, dx\\ &=\sqrt{2} \int_0^1 f(x) \, dx. \end{align}$
Illustration
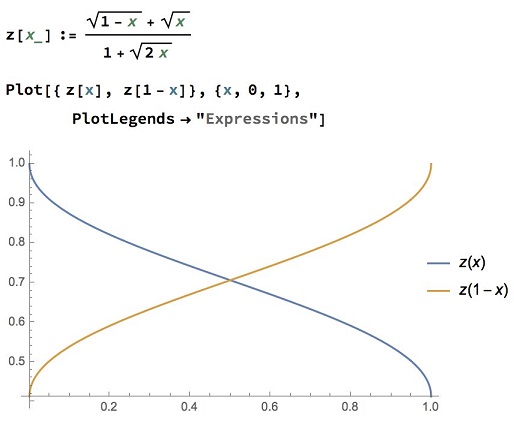
Remark
On an earlier occasion we noticed that the integrals in the form $\displaystyle \int_0^af(x)dx\,$ where $f(x)+f(a-x)=1,\,$ are always equal to $\displaystyle \frac{a}{2}.\,$ The present problem suggests a generalization:
Assume $f:\,[0,a]\to\mathbb{R}\,$ is integrable and satisfies $f(x)=g(x)h(x)\,$ where $g(x)+g(1-x)=1\,$ whereas $h(x)=h(1-x).\,$ Then
$\displaystyle \int_0^af(x)=\frac{a}{2}\int_0^ah(x)dx.$
The above solution is easily adaptable to the general case.
Adapting an example from the earlier page,
$\displaystyle\int_{0}^{10}\frac{\displaystyle (3+x^{\sqrt{7}})\sin(\frac{\pi}{2} x)dx}{6+x^{\sqrt{7}}+(10-x)^{\sqrt{7}}}=\frac{2}{\pi}.$
Acknowledgment
This problem by D. M. Bătineţu-Giurgiu and Necaulai Stanciu was previously published at the Romanian Mathematical Magazine; several additional solutions are available at the journal's web site. Solution 2 is by Amit Itagi; Solution 3 and the illustraton are by N. N. Taleb.
- A simple integral, I
- A simple integral, II
- A simple integral, III
- Another simple integral
- Yet Another Simple Integral
- Integral in Normal Distribution
- Sum Without Adding
- An Integral Inequality from the RMM
- Another Integral Inequality from the RMM
- A Triple Integral Inequality
- An Integral from the RMM
- An Integral Identity with Two Functions
- A Simple Integral of a Peculiar Function
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73611116
