An Integral Identity with Two Functions
Problem
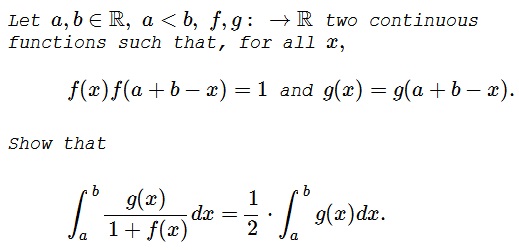
Solution
We may as well simplify the problem by choosing $a=0$ and $b=1$ so that the conditions become $f(x)f(1-x)=1$ and $g(x)=g(1-x).$ We need to prove that
$\displaystyle \int_a^b\frac{g(x)}{1+f(x)}dx=\frac{1}{2}\int_0^1g(x)dx.$
As we once observed, $\displaystyle \int_0^1u(x)dx=\int_0^1u(1-x)dx,$ for any integrable function $u=u(x).$ Thus we have
$\displaystyle \begin{align} I&=\int_0^1\frac{g(x)}{1+f(x)}dx = \int_0^1\frac{g(1-x)}{1+f(1-x)}dx \\ &= \int_0^1\frac{f(x)g(x)}{f(x)+1}dx=J \end{align}$
It is obvious that
$\displaystyle \begin{align} 2I &= I + J = \int_0^1\frac{g(x)}{1+f(x)}dx+\int_0^1\frac{f(x)g(x)}{f(x)+1}dx\\ &=\int_0^1\frac{(1+f(x))g(x)}{1+f(x)}dx=\int_0^1g(x)dx. \end{align}$
Acknowledgment
This is Problem UP.098 from the Winter 2017 Romanian Mathematical Magazine. The problem was proposed by D. M. Batinetu-Giurgiu and Neculai Staniu (Romania).
I am grateful to Dan Sitaru for providing me with a list of the problems.
- A simple integral, I
- A simple integral, II
- A simple integral, III
- Another simple integral
- Yet Another Simple Integral
- Integral in Normal Distribution
- Sum Without Adding
- An Integral Inequality from the RMM
- Another Integral Inequality from the RMM
- A Triple Integral Inequality
- An Integral from the RMM
- An Integral Identity with Two Functions
- A Simple Integral of a Peculiar Function
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73606805
