Two Colors - Three Points - Any Triangle

Prove that, in every two-coloring of the plane, there are monochromatic triangles of any shape. That is to say, there are three points of the same color that are vertices of a triangle similar to a given one.

Let the two colors be red and blue.

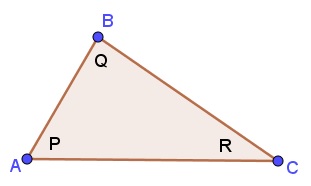
Let there be triangle $PQR;$ two of its angles are bound to be acute. Let $P$ be one of them.

Pick any to points $B$ and $C$ of the same color. At $B$ and $C$ construct angles $Q$ and $R$ and complete the triangle:

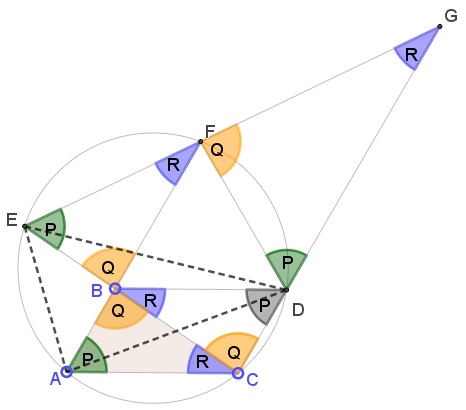
The construction proceeds as follows:

1. Complete the parallelogram $ABCD,$

2. Draw the circle $(ACD),$

3. Find $E$ and $F$ at the intersections of $(ACD)$ with $CB$ and $AB,$ respectively.

   

4. Observe that $\angle CEF=\angle CAF=P,$ while $\angle ECD=\angle BCD=Q.$ By Euclid Parallel Postulate, since $P+Q\lt 180^{\circ},$ the lines $EF$ and $CD$ meet at, say, $G.$

We have

$\begin{align} \angle CEF &=\angle CAF=P,\\ \angle EBF&=\angle ABC=Q\;\Rightarrow\; \angle AFE=R,\\ \angle CGE&=180^{\circ}-(\angle ECG+\angle CEG)=180^{\circ}-P-Q=R,\\ \angle FDG&=180^{\circ}-\angle FDC=\angle CEF=P\;\Rightarrow\;\angle DFG =Q. \end{align}$

Thus we obtain several similar triangles: $ABC,$ $CBD,$ $EBF,$ $DFG$ and $ECG.$ All are similar to the given one, $\Delta PQR.$

Recollect that points $B$ and $C$ are of the same color, say, blue. If $A$ is blue, the construction, though edifying, was unnecessary. So assume $A$ is red.

If $D$ was blue, we would have been done with $\Delta BCD.$ So assume $D$ is red.

If $E$ is blue then, assuming the worst, in $\Delta ECG,$ $G$ is red, and to avoid having $\Delta DFG$ monochromatic, we are forced to assume that $F$ is blue. But then $\Delta EBF$ is monochromatic.

If $E$ is red, then the configuration needs extension:

Note that in $\Delta AED,$ $\angle ADE=\angle ACE=R$ and

$\angle DAE=180^{\circ}-\angle DFE=180^{\circ}-(180^{\circ}-\angle DFG)=Q.$

So that $\Delta AED$ is also similar to $\Delta PQR$ and is monochromatic: all its vertices are red.

We can always find three points $A,B,C$ of the same color such that $B$ is the midpoint of $AC.$ Let $\Delta ACF$ be similar to the given one. Find the midpoints $D$ and $E$ of $AF$ and $CF,$ respectively.

We have four small and one big triangles similar to the given one. Assume $A,B,C$ are blue. If $D$ is blue, $\Delta ABD$ is monochromatic. So let $D$ be red.

If $E$ is blue $\Delta BCE$ is monochromatic. So, assume $E$ is red.

If $F$ is blue, then $\Delta ACF$ is monochromatic. So, assume $F$ is red.

But then $\Delta DEF$ is monochromatic.

This is a problem from R. Honsberger's Mathematical Delights (MAA, 2004, pp 177-178.) The problem was originally proposed by Stephen W. Knox (Mathematics Magazine, Problem 1465, February 1996). Solution is by Achilleas Sinefakopoulos.

Solution 2 trivially generalizes a particular case of monochromatic equilateral triangles that was considered separately years ago.