Pure Angle Chasing II

What Might This Be About?

Problem

Circles $(O)$ and $(Q)$ intersect in $A$ and $B;$ $C$ on $(O);$ $AC$ meets $(Q)$ second time in $D.$ $F$ - the intersection of $CO$ and $DQ;$ $E$ the intersection of the tangents to $(O)$ and $(Q)$ at $C$ and $D,$ respectively.

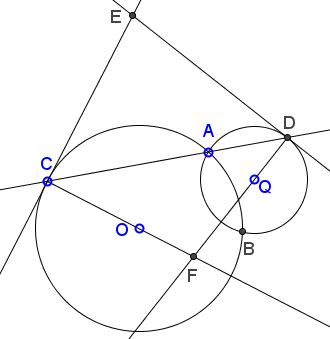
Pure Angle Chasing II - configuration

1) Prove that $EB\perp BF.$

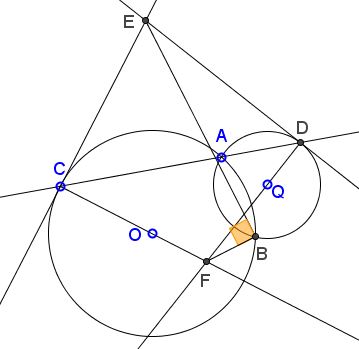
Pure Angle Chasing II - problem 1

2) Prove that points $O, F, B, Q$ are concyclic.

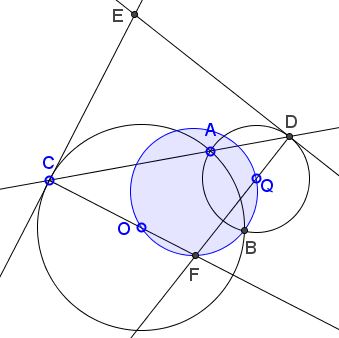
Pure Angle Chasing II - problem 2

Solution to Part 2

This is a quintessential "angle chasing".

Triangles $ACO$ and $DAQ$ are isosceles: $\angle OCA=\angle OAC$ and $\angle QAD=\angle QDA.$

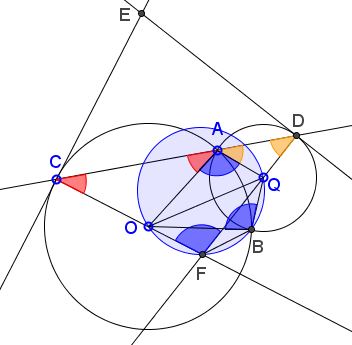
Pure Angle Chasing II - solution, problem 2

In $\Delta CDF,$

$\begin{align}\angle OFQ &= \angle CFD\\ &=180^{\circ}-\angle FCD-\angle FDC\\ &=180^{\circ}-\angle OCA-\angle QDA, \end{align}$
$\begin{align}\angle OAQ&=180^{\circ}-\angle OAC-\angle QAD\\ &=180^{\circ}-\angle OCA-\angle QDA\\ &=\angle CFD, \end{align}$
$\angle OAQ = \angle OBQ,$ because of the symmetry in $OQ.$

It follows that $\angle OFQ = \angle OBQ,$ implying that the four points $O,F,B,Q$ are concyclic.

Solution to Part 1

Observe that $\angle CBD$ does not depend on a specific position of $C.$

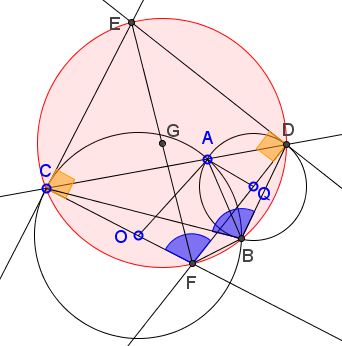
Pure Angle Chasing II - solution, problem 1

Further,

$\begin{align}\angle CBD &= \angle CBA + \angle ABD\\ &=\angle ACE+\angle ADE\\ &=180^{\circ}-\angle CED. \end{align}$

So that $B$ lies on circle $CDE.$ But, since $\angle ECF=\angle EDF=90^{\circ},$ this is exactly the circle with diameter $EF.$

Angle $EBF$ being subtended by a diameter of $(CFBDE)$ is, therefore, right.

Looking back

With the dynamic diagram it is hardly possible to miss the fact that the center of $(CED)$ lies on $(OFBQ).$

First of all, observe that circle $(OFBQ)=(OBQ)$ is stationary - it does not depend on the position of $C.$

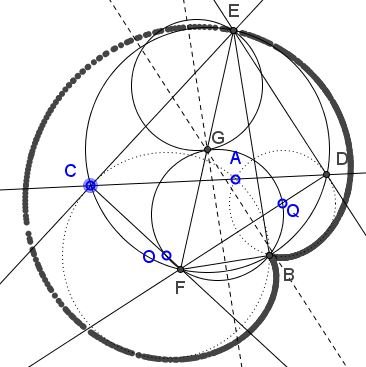
Pure Angle Chasing II - solution, problem 1

As point $F$ traces the $(OBQ)$ circle, the perpendicular bisector of $BF$ meets the circle at $G,$ and the reflection $E$ of $F$ in $G$ traces a cardioid with the cusp at $B.$ This is quite suggestive and looks good, but does not answer the question: the fact is that the center of $(CED)$ lies on $(OBQ)$.

One possibility to prove that is to show that the perpendicular bisectors of $BF$ and $BD$ meet on $(OBQ).$ As Murray Klamkin once wrote "small solved and unsolved problems lead to larger solved and unsolved problems..." I'll treat that problem separately.

Let there be two circles $(P)$ and $(Q),$ with $Q$ on $(P);$ $F$ a point on $(P);$ $D$ an intersection of $FQ$ with $(Q).$

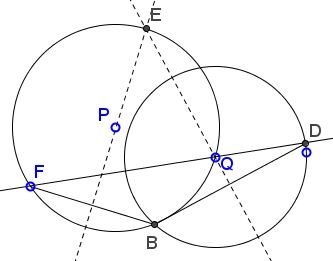
Pure Angle Chasing II - another problem

Prove that the intersection $E$ of the the perpendicular bisectors of $BF$ and $BD$ lies on $(P).$

Acknowledgment

I borrowed the basic problem from Antonio Gutierrez after he broadcasted it at tweeter.com.

Chasing Inscribed Angles

71536666