Reim's Similar Coins II
What Might This Be About?
Problem
Let two circles cross at points $A$ and $B;$ $E$ and $F$ are two points on one of the circles, $G$ and $H$ on the other. Assume $AG\parallel FB$ and $BH\parallel EA.$
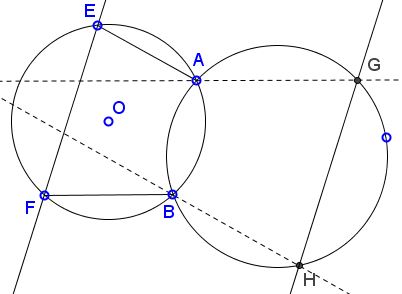
Then $GH\parallel EF.$
Solution
Chasing angles leads to a simple solution.

As a pair of vertical angles in parallel lines $(AG\parallel FB),)$ $\angle ABF=\angle BAG.$ Further, since quadrilaterals $ABFE$ and $ABHG$ are cyclic, $\angle ABF+\angle AEF=180^{\circ}$ and also $\angle BAG+\angle BHG=180^{\circ},$ implying $\angle AEF=\angle BHG.$ These two angles have one pair of sides parallel $(BH\parallel EA.)$ So their other sides are also parallel, $GH\parallel EF.$
Converse 1
Given a cyclic quadrilateral $ABFE$ and points $G$ and $H$ such that $AG||FB$ and $BH\parallel EA.$ If $GH\parallel EF,$ then quadrilateral $ABHG$ is cyclic.

Converse 2
Let two circles cross at points $A$ and $B;$ $E$ and $F$ are two points on one of the circles; $AG||FB$ whereas chord $GH$ is parallel to $EF.$

Then $BH\parallel EA.$
For, if $BH'||AE,$ with $H'$ on the second circle, then $GH'\parallel EF\parallel GH,$ implying that $H=H'.$
Acknowledgment
I confess to not knowing the reason for the theorem designation. There is a companion theorem under the same attribution. I came across this one in an article by Jean-Louis Ayme where he referred to it as "Le théorème des moniennes semblables de Reim" which both I and google had a difficulty translating. It looks to me like "Reim's similar coins" might be a good fit, but I am not sure.
Chasing Inscribed Angles
- Munching on Inscribed Angles
- More On Inscribed Angles
- Inscribed Angles
- Tangent and Secant
- Angles Inscribed in an Absent Circle
- A Line in Triangle Through the Circumcenter
- Angle Bisector in Parallelogram
- Phantom Circle and Recaptured Symmetry
- Cherchez le quadrilatere cyclique
- Cyclic Quadrilateral, Concurrent Circles and Collinear Points
- Parallel Lines in a Cyclic Quadrilateral
- Reim's Similar Coins I
- Reim's Similar Coins II
- Reim's Similar Coins III
- Reim's Similar Coins IV
- Pure Angle Chasing
- Pure Angle Chasing II
- Pure Angle Chasing III
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579832
