Pure Angle Chasing III

The problem is somewhat ambiguous: in general, two circles or a circle and a line have two points of intersection. It more or less clear that selection a point of intersection of $(P)$ and $(Q)$ and denoting it $B$ would not make much difference. Because of the symmetry, what is true for one of the points, is true for the other.

It is less clear, in my view, that the same holds for the two points of intersection of $FQ$ with $(Q)$ because their locations (one within $(P),$ the other without) are essentially different. To be safe, let's denote $D'$ the second intersection of $FQ$ with $(Q).$

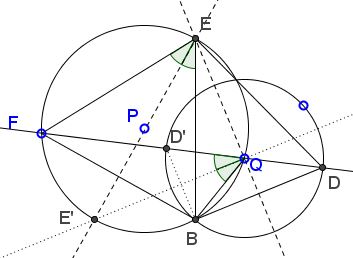
We need to show that the intersection $E$ of the perpendicular bisectors of $BF$ and $BD$ lies on $(P).$ Let's relax the problem and define $E$ as the intersection of the perpendicular bisector of $BD$ with $P.$ This reduces the task to showing that the perpendicular bisector of $BF$ passes through $E.$

Now, we'll see that the introduction of $D'$ was a wise step. Let $E'$ be the second intersection of the bisector of $BD'$ with $(P).$

By the construction, $\angle DBD'$ inscribed in $(Q)$ is subtended by the diameter $DD'$ is right, implying $\angle EQE'=90^{\circ}.$ This is because, having $\angle DBD'=90^{\circ},$ $EQ\perp BD,$ and $E'Q\perp BD',$ shows that $E'Q\parallel BD$ and $EQ\parallel BD'.$

This makes $EE'$ a diameter of $(P).$ Therefore, if one of $E$ and $E'$ divides one of the arcs $BF$ in $(P),$ the other divides the second arc.

Now, $E'Q$ being a perpendicular bisector of $BD',$ $\angle D'QE'=\angle BQE'$ such that the arcs $FE'$ and $E'B$ in $(P)$ are equal: $E'$ is the midpoint of $\overparen{BF}.$ And so is $E$ (but of the second arc $BF.)$ This shows that $EE'$ is indeed the perpendicular bisector of $BF.$

This is an outgrowth of an earlier problem.