Reim's Similar Coins III
What Might This Be About?
Problem
Let two circles cross at points $A$ and $B;$ $E,F,E'F'$ are four points on one of the circles, $EA$ and $E'B$ meet the other circle at $H$ and $H',$ respectively; $FB,F'A$ meet it at $G$ and $G',$ respectively. Assume $EF\parallel E'F'.$
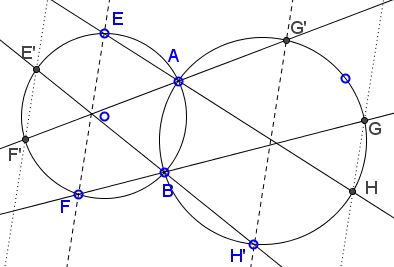
Then $GH\parallel EF\parallel E'F'\parallel G'H'.$
Solution
The problem can be solved directly, as suggested by the diagram below.
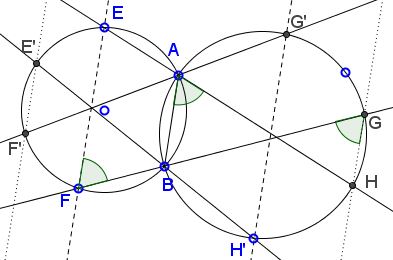
But, in fact, it is a direct consequence of Reim's Similar Coins theorem.
Chasing Inscribed Angles
- Munching on Inscribed Angles
- More On Inscribed Angles
- Inscribed Angles
- Tangent and Secant
- Angles Inscribed in an Absent Circle
- A Line in Triangle Through the Circumcenter
- Angle Bisector in Parallelogram
- Phantom Circle and Recaptured Symmetry
- Cherchez le quadrilatere cyclique
- Cyclic Quadrilateral, Concurrent Circles and Collinear Points
- Parallel Lines in a Cyclic Quadrilateral
- Reim's Similar Coins I
- Reim's Similar Coins II
- Reim's Similar Coins III
- Reim's Similar Coins IV
- Pure Angle Chasing
- Pure Angle Chasing II
- Pure Angle Chasing III
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73572384
