Angle Bisector in Parallelogram
What Is It About?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener| |Store|
Copyright © 1996-2015 Alexander Bogomolny
Angle Bisector in Parallelogram
The applet illustrates Problem 2 from IMO 2007:
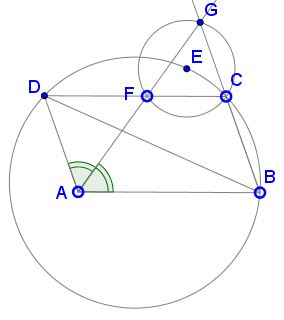
Consider five points A, B, C, D and E such that ABCD is a parallelogram and BCED is a cyclic quadrilateral. Let l be a line passing through A. Suppose that l intersects the interior of the segment DC at F and intersects line BC at G. Suppose also that
| Buy this applet What if applet does not run? |
The solution is an adaptation of that by Anton Batominovski (a simpler variant appears elsewhere.)
The condition EF = EG = EC is equivalent to E being the circumcenter of ΔCFG. Thus we shall prove a stronger result:
Consider five points A, B, C, D and E such that ABCD is a parallelogram and BCED is a cyclic quadrilateral. Let l be a line passing through A. Suppose that l intersects the interior of the segment DC at F and intersects line BC at G. The circumcenter E of ΔCFG lies on the circumcircle of ΔBCD if and only if l bisects ∠DAB.
Assume first that l is the bisector of ∠BAD. This makes ΔABG isosceles so that
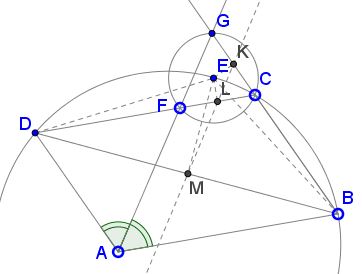
ΔFCG is also isosceles (and similar to ΔABG.) In particular, EC being its apex altitude and angle bisector,
∠ECF = ∠ECG.
Bt, since E is the circumcenter of ΔCFG, ΔCEG is isosceles,
Now let's prove the converse. Assume E lies on the circumcircle of ΔBCD. By the Simson-Wallace Theorem theorem, the feet of the perpendiculars EK, EL, EM from E to the sides BC, CD, BD are collinear on the Simson line, where K is the midpoint of CG, while L is the midpoint of CF. The homothety with center C and coefficient 2 maps K onto G, L onto F, the line KL onto l, and the diagonal BD onto a parallel line through A. M being on the two lines is mapped to the intersection of their images, which is A. This makes M the midpoint of the diagonal AC and, as a consequence, also the midpoint of the diagonal BD. ΔBED is then isosceles, with
On the other hand, ∠DBE = ∠DCE (as inscribed angles subtended by the same chord). Also, since BCDE is cyclic, ∠BDE is supplementary to ∠BCE as is ∠GCE so that
∠DCE = ∠GCE
making CE an angle bisector in ΔCFG. But since E is the circumcenter of ΔCFG it also becomes the altitude and the median from C which means that ΔCFG is isosceles as are triangles ADF and ABG. All three are similar and we finally get
|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener| |Store|
Copyright © 1996-2015 Alexander Bogomolny
| 49551934 |
