Two Diameters and Longest Common Chord

Circles \((A)\) and \((B)\) intersect in two points \(M\) and \(P\). A common chord \(DE\) is drawn through \(M\) with \(D\) on \((B)\) and \(E\) on \((A)\).

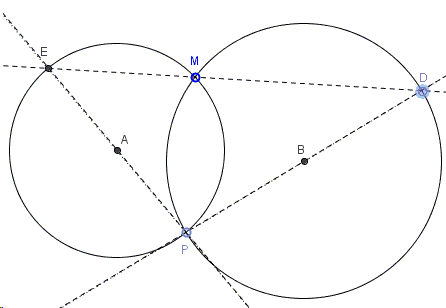
Two circles intersect. The end points joined to the other common point. If one segment a diameter, so it the other

Prove \(EP\) is a diameter of \((A)\) if and only if \(DP\) is a diameter of \((B).\)

(The applet below illustrates the problem.)

Created with GeoGebra

Solution

Circles \((A)\) and \((B)\) intersect in two points \(M\) and \(P\). A common chord \(DE\) is drawn through \(M\) with \(D\) on \((B)\) and \(E\) on \((A)\).

Two circles intersect. The end points joined to the other common point. If one segment a diameter, so it the other

Prove \(EP\) is a diameter of \((A)\) if and only if \(DP\) is a diameter of \((B).\)

Solution

Note that the angles in \(\Delta DEP\) do not depend on the position of point \(D\), for angles at \(D\) and \(E\) are inscribed and always subtended by the same chords. Among all triangles \(DEP\) the largest has the largest possible side \(DP,\) which is exactly the diameter of \((B).\) Applying this same argument in \((A)\) shows that for the largest \(\Delta DEP,\) \(EP\) is a diameter of \((A).\)

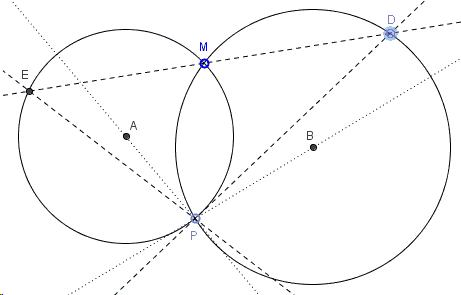
Two circles intersect. The end points joined to the other common point. If one segment a diameter, so it the other - solution

This is a redux of the problem that required to find the longest common chord (\(D'F'\) in this case) of two intersecting circles.

71535736