Pure Angle Chasing

What Might This Be About?

Problem

Circles $(O)$ and $(Q)$ intersect in $A$ and $B;$ $C$ on $(O);$ $AC,$ $BC$ meet $(Q)$ second time in $D$ and $E,$ respectively.

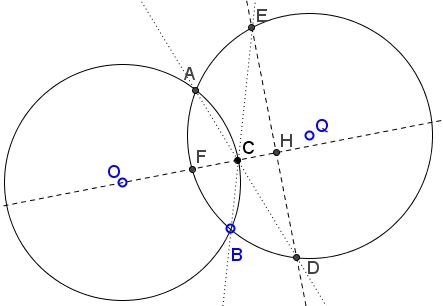
Pure Angle Chasing - problem

Prove that $OC$ is perpendicular to $DE.$

Solution 1

This is a quintessential "angle chasing".

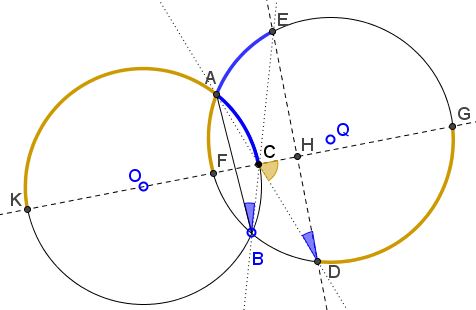
Pure Angle Chasing - solution

We use properties of inscribed angles. Let $OC$ meet $(Q)$ in $F$ and $G$ and $(O)$ in $K$ as shown. Let $H$ be the intersection of $OC$ and $DE.$ Then

$\displaystyle \angle CDH=\angle ADE=\angle ABE=\angle ABC=\frac{1}{2}\overparen{AC},$
$\displaystyle \angle DCH=\angle ACK=\frac{1}{2}\overparen{AK}.$

It follows that $\displaystyle\angle CDH+\angle DCH=\frac{1}{2}\overparen{CK}=90^{\circ}.$ But then (from $\Delta CDH)$ $\angle CHD =180^{\circ}-(\angle CDH+\angle DCH)=90^{\circ}.$

Solution 2

Machò Bònis posted another solution at the Cut the Knot facebook page:

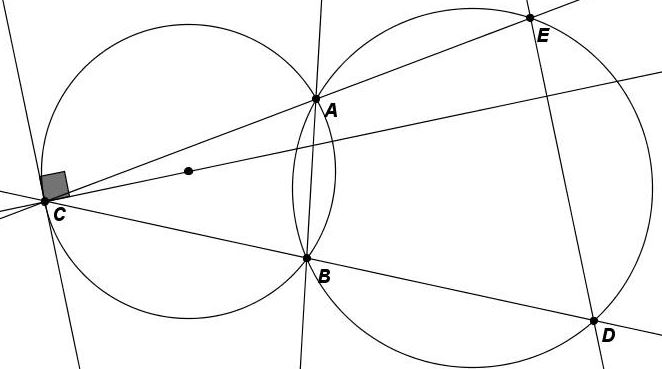
Pure Angle Chasing - solution 2

Draw a tangent to $(O)$ at $C.$ The result follows immediately by a limiting case of Reim's theorem.

Acknowledgment

I borrowed this problem from Antonio Gutierrez after he broadcasted it at tweeter.com.

Chasing Inscribed Angles

71542567