Reim's Similar Coins IV
What Might This Be About?
Problem
Given a cyclic quadrilateral $ABFE,$ let $AG$ and $BH$ be extended away from $ABFE$ so that
- $\angle EAG=\angle FBH,$ but measured in opposite directions,
- $GH\parallel EF.$
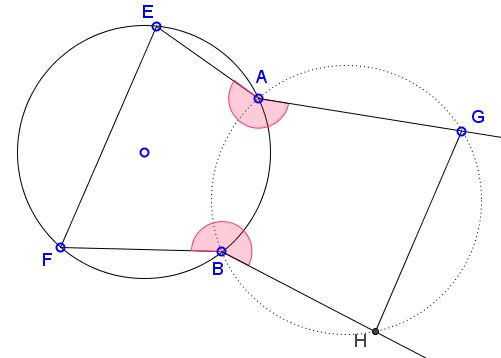
Then quadrilateral $ABHG$ is cyclic.
Solution
Draw circle $(ABG).$ We need to show that $H$ lies on that circle.
Find $G'$ on $(ABG)$ such that $AG'\parallel FB.$ Add $H'$ on $(ABG),$ with $G'H'\parallel EF.$ By one of Reim's theorems, $FH'$ passes through $B.$ By the construction, $\angle FBH'=\angle EAG'$ so that also $\angle HBH'=\angle GAG'.$
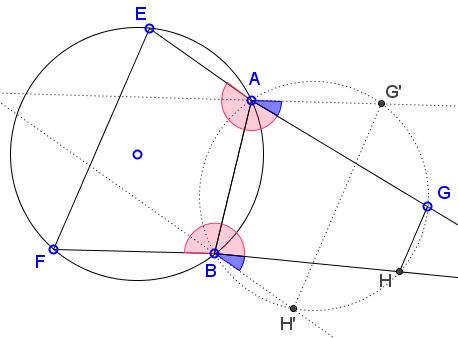
If $H''$ is the intersection of $GH$ with circle $(ABG)$ then $\overparen{H'H''}=\overparen{GG'}$ from which $GH''\parallel G'H',$ implying $H=H''.$ It follows that the points $A,B,H,G$ are indeed concyclic.
Chasing Inscribed Angles
- Munching on Inscribed Angles
- More On Inscribed Angles
- Inscribed Angles
- Tangent and Secant
- Angles Inscribed in an Absent Circle
- A Line in Triangle Through the Circumcenter
- Angle Bisector in Parallelogram
- Phantom Circle and Recaptured Symmetry
- Cherchez le quadrilatere cyclique
- Cyclic Quadrilateral, Concurrent Circles and Collinear Points
- Parallel Lines in a Cyclic Quadrilateral
- Reim's Similar Coins I
- Reim's Similar Coins II
- Reim's Similar Coins III
- Reim's Similar Coins IV
- Pure Angle Chasing
- Pure Angle Chasing II
- Pure Angle Chasing III
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573652
