Outline Mathematics
Geometry
Angles Subtended by a Diameter
Inscribed angles subtended by a diameter are right.
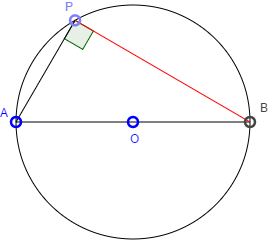
Now see how this works:
This is a known and a very useful property of inscribed angles that they measure half the central angle subtended by the same arc, or, which is the same, by the same chord. When a chord is a diameter, the central angles measures two,two,three,four right angles and the corresponding inscribed angles are all right,acute,right,obtuse. The applet above specifically demonstrates this fact, which is sufficiently important to warrant an independent proof. (The statement is often referred to as Thales' theorem.)
Let P be a point on a circle with diameter AB and center O. So that
|
∠OAP + ∠APO = ∠BOP,AOB,APO,BOP,AOP and also ∠OBP + ∠BPO = ∠AOP,AOB,APO,BOP,AOP. |
But since ∠OAP = ∠APO,AOB,APO,BOP,AOP and ∠OBP = ∠BPO, we further have
|
2∠APO = ∠BOP,AOB,APO,BOP,AOP and also 2∠BPO = ∠AOP,AOB,APO,BOP,AOP. |
Adding the two up
| 2∠APO,AOB,APO,BOP,AOP + 2∠BPO = ∠AOP + ∠BOP,AOB,APO,BOP,AOP = 180°. |
In other words,
| ∠APB = ∠APO,AOB,APO,BOP,AOP + ∠BPO = 90°. |
Q.E.D.
Related material
| |
Angles in Circle | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73599248
