Line Not Through a Center of Similarity
What is this about?
Problem
A straight line meets circles $(O_{1})$ and $(O_{2}),$ centered at $O_{1}$ and $O_{2},$ respectively, at points $A_{i}$ and $B_{i},$ $i=1,2.$ The tangents to the circles at these points cross at four points, $X,\,Y,\,Z,\,W.$
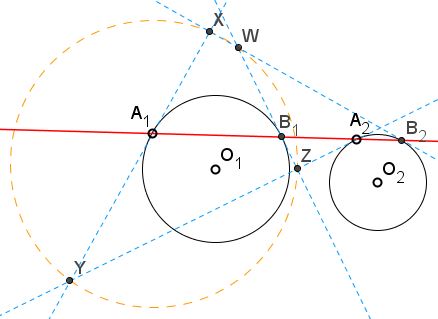
Prove that the four points are concyclic.
Solution
The angle between a chord and a tangent at one of the chord's endpoints equals half the central angle subtended by the chord. This, in part, implies that the angles at the endpoints are equal. Let $\alpha_{1}$ be the angle at $A_{1},\,B_{1},$ $\alpha_{2}$ be the angle at $A_{2},\,B_{2}.$
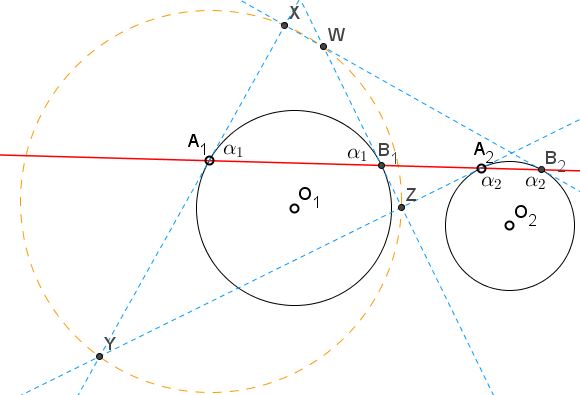
In $\Delta A_{1}A_{2}Y,$ by the Law of Sines,
$\displaystyle\frac{A_{1}Y}{A_{2}Y}=\frac{\mbox{sin}\angle A_{1}A_{2}Y}{\mbox{sin}\angle A_{2}A_{1}Y}=\frac{\mbox{sin}\alpha_{2}}{\mbox{sin}(\pi -\alpha_{1})}=\frac{\mbox{sin}\alpha_{2}}{\mbox{sin}\alpha_{1}}.$
This means that $Y$ lies on the circle of Apollonius constructed for the centers $(O_{1})$ and $(O_{2}),$ and the ratio $k=\displaystyle\frac{A_{1}Y}{A_{2}Y}=\frac{\mbox{sin}\alpha_{2}}{\mbox{sin}\alpha_{1}}.$ This is also true for the remaining intersections $X,\,Z,\,W.$ Thus all four points are concyclic - they lie on a circle of Apollonius. Incidentally, the center $(O)$ of their circumcircle is lies on the line of centers $O_{1}O_{2}.$
Note: The case where the given line does pass through one of the centers of similarity is treated on a separate page.
Acknowledgment
This is problem 251b from the second volume of I. M. Yaglom's Geometric Transformations, Russian edition (1956.) I am pretty sure that the problem has been included in the fourth volume of the English translation, but not owning the book I am unable to verify that fact.
The Circle of Apollonius
- Locus of Points in a Given Ratio to Two Points
- Line Not Through a Center of Similarity
- A View on the Circle of Apollonius
- Coaxal Circles Theorem
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581125
