Angle Chasing in a 75-30-75 triangle
Problem
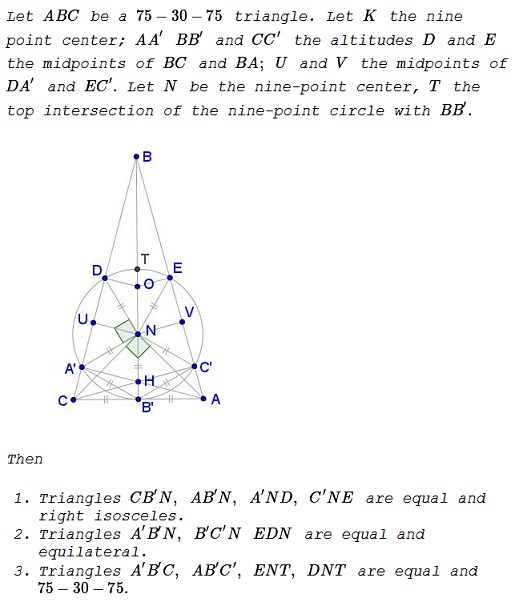
Solution
We shall be using trigonometric functions of $15^{\circ}:\,$ $\sin (15^{\circ})=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{2}\,$ $\tan (15^{\circ})=2-\sqrt{3}.\,$ As an afterthought, $\tan (75^{\circ})=2+\sqrt{3}.$
Let's choose the coordinate system with horizontal $x-\text{axis}\,$ and vertical $y-\text{axis}\,$ such that $B'=(0,0),\,$ $C=(-2,0),\,$ $A=(2,0),\,$ $B=(0, 2(2+\sqrt{3})).$
Then $E=(1,2+\sqrt{3}),\,$ $D=(-1,2+\sqrt{3}).\,$ $CC'\,$ is defined by $y=(2-\sqrt{3})(x+2)\,$ and $AA'\,$ by $y=-(2-\sqrt{3})(x-2).\,$ Note that, for both, $y(0)=2-\sqrt{3},\,$ such that $H=(0,2-\sqrt{3}).\,$ The equation of $BC\,$ is $y=(2+\sqrt{3})(x+2)\,$ which gives $A'=(-\sqrt{3},1)\,$ as its intersection with $AA'.\,$ Similarly, $C'=(\sqrt{3},1).\,$
$V=\displaystyle\frac{E+C'}{2}=\left(\frac{1+\sqrt{3}}{2},\frac{3+\sqrt{3}}{2}\right).\,$ The equation of the perpendicular to $AB\,$ at $V\,$ is $\displaystyle y=(2-\sqrt{3})\left(x-\frac{1+\sqrt{3}}{2}\right)+\frac{3+\sqrt{3}}{2}.\,$ $y(0)=2,\,$ so that $N=(0,2),\,$ making $\Delta AB'N\,$ right isosceles. Same for $\Delta CB'N.\,$ As a consequence, $\angle ANC=90^{\circ}.$
To see that $\angle C'NE=90^{\circ}\,$ we apply matrix $T=\left(\begin{array}{cc}\,0&-1\\1&0\end{array}\right),\,$ which is the counterclockwise rotation through $90^{\circ},\,$ to vector $\overrightarrow{NV}=\left(\begin{array}{c}\sqrt{3}\\-1\end{array}\right)\,$ and place it at $N:$
$\left(\begin{array}{cc}\,0&-1\\1&0\end{array}\right)\left(\begin{array}{c}\sqrt{3}\\-1\end{array}\right)+\left(\begin{array}{c}0\\2\end{array}\right)=\left(\begin{array}{c}1\\\sqrt{3}\end{array}\right)+\left(\begin{array}{c}0\\2\end{array}\right)=\left(\begin{array}{c}1\\2+\sqrt{3}\end{array}\right)\,$
which is point $E.\,$ Similarly, $\angle A'ND=90^{\circ}.\,$ To establish the rest of the claims, suffice it to show that $\angle A'NC'=120^{\circ}.\,$ he counterclockwise rotation through $120^{\circ}\,$ is defined by the matrix
$\displaystyle S=\frac{1}{2}\left(\begin{array}{cc}\,-1&\,-\sqrt{3}\\\sqrt{3}&-1\end{array}\right).\,$
Thus, we compute $S\cdot\overrightarrow{A'N}+N:$
$\displaystyle =\frac{1}{2}\left(\begin{array}{cc}\,-1&-\sqrt{3}\\\sqrt{3}&-1\end{array}\right)\left(\begin{array}{c}\,-\sqrt{3}\\-1\end{array}\right)+\left(\begin{array}{c}0\\2\end{array}\right)=\left(\begin{array}{c}\,\sqrt{3}\\1\end{array}\right),$
which is $C'.$
Acknowledgment
This page should be considered as a companion of the one on the Nine Point Center in Square. It is more of what was discerned on that page by Leo Giugiuc, Takis Chronopoulos, Amit Itagi and I than an independent material.
The problem offers a nice exercise in the beginning analytic geometry and even linear algebra.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581651
