Isoperimetric Theorem for Quadrilaterals II
Illustration
Introduction
Among all quadrilaterals with the same perimeter, square has the largest area.
or, equivalently,
Among all quadrilaterals with the same area, square has the smallest perimeter.
If $P$ is the perimeter and $A$ area of a $2D$ figure, then, for square, $P^{2}=16A.$ The above statement, known as isoperimetric theorem is equivalent to the inequality, $P^{2}\ge 16A,$ for any quadrilateral, with equality only for square.
For a non-convex quadrilateral, one of the diagonals passes in its exterior. If, say, $AC$ is such a diagonal, then quadrilateral $ABCD',$ where $D'$ is the mirror image of $D$ in $AC,$ has the same perimeter as $ABCD$ but larger area, obviously.
For convex quadrilateral, the proof proceeds in three steps. Starting with an arbitrary quadrilateral, which is not a kite, we'll find a kite with the same perimeter but larger area. For a kite which is not a rhombus, we'll find a rhombus with the same perimeter but larger area. Finally, for a rhombus which is not a square, we'll find a square with the same perimeter but larger area.
I shall use $[X]$ to denote the area of shape $X.$
Quadrilateral to kite
If, for example, $AD\ne CD,$ draw an ellipse with foci at $A$ and $C$ passing through $D$. Let the perpendicular bisector of $AC$ cross the ellipse in $D'$ on the same side of the axis $AC$ as $D.$ Then $AD+CD=AD'+CD'$ but, in addition, $[ACD']\gt [ACD]$ because the two triangles have the same base $AC$ with the altitude of one longer than that of the other.
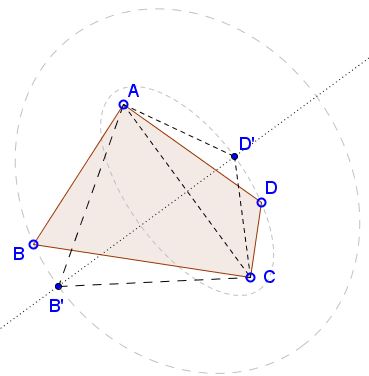
In case $AB=BC$ we may proceed to the next step. If not, as before, we draw an ellipse with foci at $A$ and $C$ passing through $B$ and find $B'$ such that $AB+BC=AB'+B'C$ and $[ACB']\gt [ACB].$
Putting the triangles together we see that $AB'CD'$ has the same perimeter as $ABCD$ but larger area.Kite to rhombus
We start with quadrilateral $AB'CD'$ in which $AB'=B'C$ and $AD'=CD'.$ If, say, $AB'=AD'$ the quadrilateral is a rhombus and we may proceed to the next step. If not, draw an ellipse with foci at $B'$ and $D'$ and passing through $A$. By symmetry, $C$ will also lie on th ellipse.
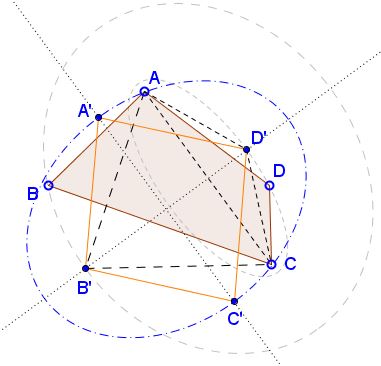
As on the previous step me may choose $A'$ (and simultaneously $C'$) such that $A'B'C'D'$ has the same perimeter as $AB'CD'$ but larger area while having all four sides equal.
Rhombus to square
Given rhombus $A'B'C'D',$ consider the areas of two triangles $A'B'D'$ and $B'C'D'.$ Their areas are half the product of their bases $A'B'$ and $B'C'$ by their respective altitudes $D'E$ and $D'F.$ Both altitudes do not exceed the sides $A'D'$ and $C'D'$ of the triangles. They are equal to the side only when $A'B'C'D'$ is a square.

Acknowledgment
The proof is due to A. M. Fink (The Mathematical Gazette, v 98, n 543 Nov 2014, 504) from Iowa State University.
An alternative proof proceeds through the sequence
$quadrilateral\rightarrow parallelogram\rightarrow rectangle\rightarrow square.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73598103
