Isoperimetric Theorem for Parallelograms

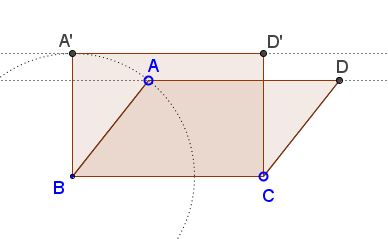
Indeed, according to Euclid I.35, parallelograms with the same base and in the same parallels have equal areas. Restricting to rectangles, it is clear that, among rectangles with the same base, the area grows with the distance between the parallel lines. Since in a circle, the point farthest from a diameter, lies on the perpendicular radius, the area of a rectangle among all parallelograms with the same sides is the largest.

The above has been communicated to me in private correspondence by Sidney Kung on 1 March, 2014.