An Isoperimetric Problem in Quadrilateral

By a variant of the isoperimetric theorem, among all quadrilateral of given area square has the smallest perimeter. Thus, for one, for any quadrilateral of area $1,$ $AB+BC+CD+DA\ge 4,$ the perimeter of the square of area $1.$

On the other hand, the area of quadrilateral $ABCD$ is $\displaystyle [ABCD]=\frac{1}{2}AC\cdot BD\cdot\sin\angle (AC,BD).$ This is half the area of the parallelogram $ACFE$ formed on the diagonals $AC$ and $BD.$

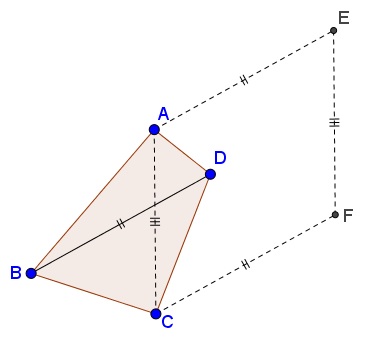
Thus $[ACFE]=2.$ Square of side $\sqrt{2}$ has the smallest perimeter $4\sqrt{2}$ of all quadrilaterals with the area of $2.$ Thus, $2(AC+BD)\ge 4\sqrt{2},$ or $AC+BD\ge 2\sqrt{2}.$

Combining the two inequalities gives

$\displaystyle (AB+BC+CD+DA)+(AC+BD)\ge 4+2\sqrt{2}.$

But the inequality reduces to equality for a square, implying that the required minimum is exactly $4+2\sqrt{2}.$

This may be called Isodiagonal Theorem:

The sum of the diagonals of any convex quadrilateral of area $1$ is at least $2\sqrt{2}.$ In other words, among all convex quadrilaterals of area $1$ square has the least sum of the diagonals.

Let $AB = a,$ $BC = b,$ $CD = c,$ $DA = d$ and $\displaystyle s=\frac{a + b + c + d}{2},$ so that $\displaystyle a+b+c+d=\sum_{cycl}(s-a).$ By The AM-GM inequality then,

$a + b + c + d \ge 4\sqrt[4]{(s - a)(s - b)(s - c)(s - d)}=4\sqrt{[ABCD]}=4.$

Also, $AC + BD = 2\sqrt{AC\cdot BD} = 2\sqrt{2[ABCD]} = 2\sqrt{2}.$ Thus, $a + b + c + d + AC + BD = 4 + 2\sqrt{2}.$ Note that if $ABCD$ is a square of side 1, then $a + b + c + d + AC + BD = 4 + 2\sqrt{2}.$

Leo Giugiuc has kindly messaged me this problem along with his solution (Solution 2) but with a wrong reference to NMTC 2017. Thus the search for the source of the problem is on.